��^�̏����������m�C�Y�ɂȂ�܂�
�@���������ȃ^�C�g���ł����ǁA�Ō�ɈӖ����킩��܂��B�Ƃ肠���������y = (logx)2
�Ƃ��������x�[�X�ɘb��i�߂܂��B���̊��͂���܂łɂ����x���o�ꂵ�܂������A���߂ăO���t���ڂ��Ă����܂��B
�@
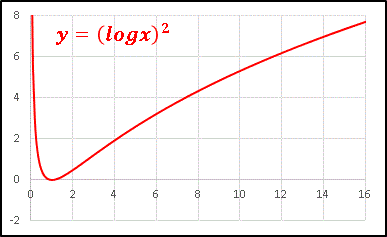
�@logx �� cosx ���|���� 2 �悷��ƁA y = (logx)2 �ɉ������`�̐U�����������܂��F
�@
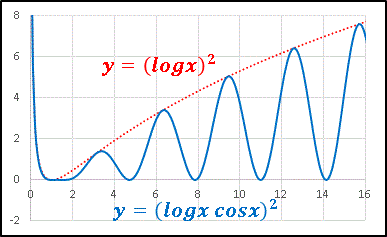
�@(logx)2 ���� sin2x ��������
y = (logx)2 �| sin2x
�Ƃ�����������ăO���t��`���Ă݂�� ......
�@
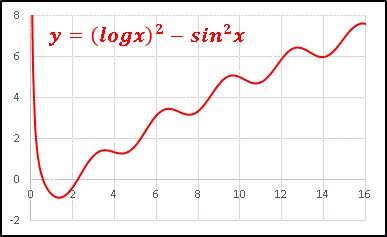
�@�O�p���̉e���� �O���t�S�̂������݂ɗh��܂��B
�@���̊��S�̂� cos(x/��) ���|����
y = [(logx)2 �| sin2x] cos(x/��)
�Ƃ�����������Ă݂�� ......
�@
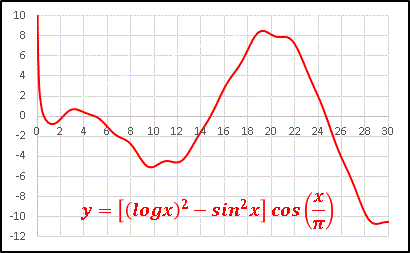
�@�����̗\����������G�Ȋ��ɂȂ�܂��B
�@�ׂ����h��� sin2x �̉e���ł�����A�������菜����
y = (logx)2 cos(x/��)
�Ƃ��Ă݂�� ......
�@
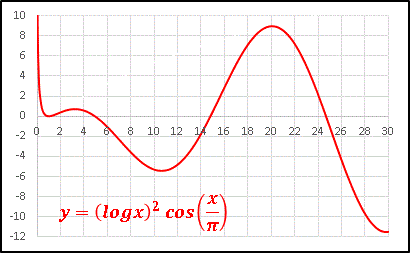
�@��������Ƃ����`�̃O���t�ɂȂ�܂��B����Ȃ�R���s���[�^���g��Ȃ��Ă��[���ɉ�͂ł���Ղ������ł��B sin2x �� 0 �` 1 �̒l�����Ƃ�܂���A�m�C�Y�̂悤�ɍׂ����U�������� ���ʂ�������܂���B�������G�Ȋ������������Ƃ��ɂ́A��^�̏�����������蕥���Ă݂邱�ƂőS�̂̐�����m�邱�Ƃ��ł��܂��B
�@ �@