Excel �łȂ��炩�Ȏ������ƃW�O�U�O�O�p�`�̃O���t��`���܂�
�@����� y = cos[x + cosx] �Ƃ��������x�[�X�ɂ��܂��B�@cos �̒��� cosx ������q�ɂȂ��Ă��܂��ˁB�O���t��`���Ă݂�� ......
�@
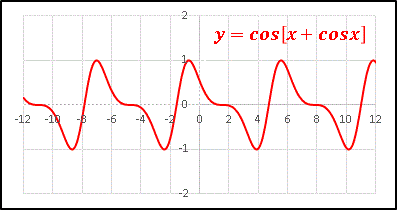
�@�������ςȔg�`�ł����A�Ƃ��������������ł��B
�@�����č��x�� [�@] �̒��� cosx �� x ������� cosx �Œu��������
y = cos[x + cos(cosx)]
�Ƃ��܂��B��������� cos ���ǂ�ǂ����q�ɂ��Ă����̂ł����Acos �����炸��ƕ��ԂƖڂ����炿�炷��̂ŁA
�@f2(x) = cos(cosx)
�@f3(x) = cos(cos(cosx))
�̂悤�ɏ������Ƃɂ��܂��By = cos[x + f2(x)] �� ......
�@
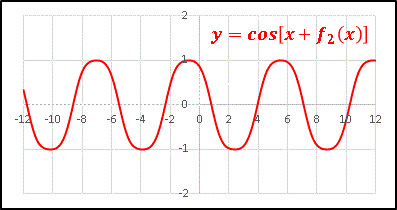
�@���x�͒P���łȂ��炩�Ȏ������ƂȂ�܂����B
�@������ y = cos[x + f3(x)] �����Ă݂܂��傤�B
�@
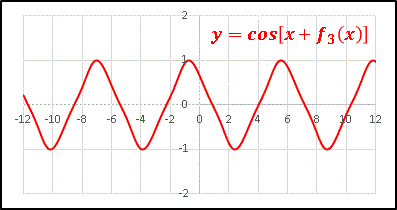
�@������ƃW�O�U�O�����O�p�`������ł��܂��ˁB
�@y = cos[x + f4(x)] �͂ǂ��Ȃ�ł��傤�H
�@
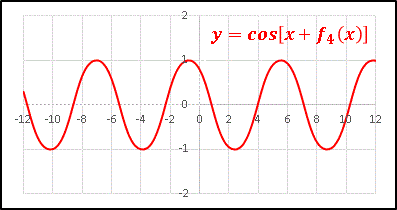
�@����B�܂����炩�Ȏ������ɖ߂��Ă��܂��܂����B
�@�Ō�� y = cos[x + f5(x)] �̃O���t��`���Ă݂܂��B
�@
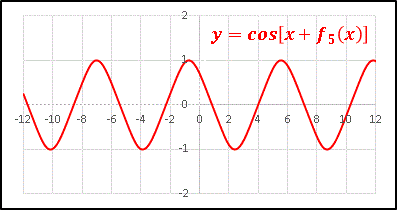
�@���x�͂��ꂢ�ȎO�p�`�����т܂����ˁI
�@
���������Ă݂܂�
�@������ sin �̕ϐ����������ŗ}�����܂�Ă���� x �̑����ɍ��킹�ď����������������Ȃ�܂��B�t�ɕϐ��� 2 �悷��Ύ������Z���Ȃ��Ă����܂��F�@
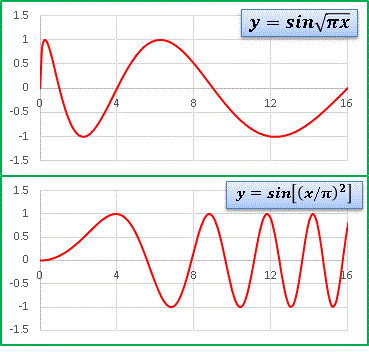
�@�ł͂��̂Q��ނ̕ϐ����d�݂����ďd�ˍ��킹��
�̂悤�Ȍ`�ɂ���Ǝ����̐U�镑����F�X�ƕς���ꂻ���ł��ˁB
a, b ��ω������ăO���t��`���Ă݂܂��傤�F
�@
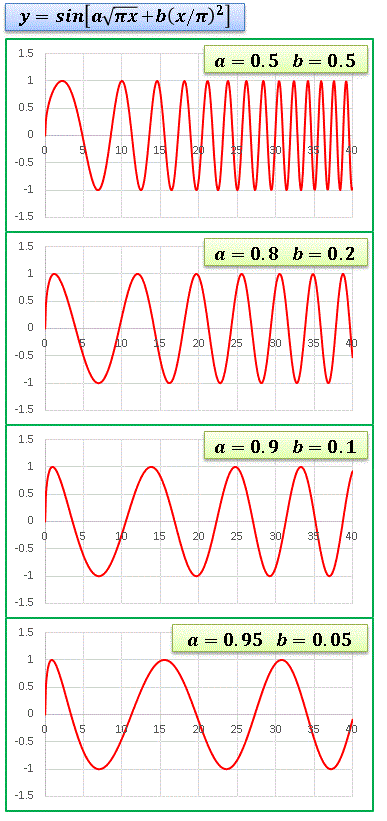 �@
�@�@�P�ԏ�̐}�ł͓������d�݁ia = 0.5, b = 0.5�j�����ďd�˂Ă���܂����A��x �̍����� x 2 �̍��̂ق��������������̂ŁA���Ȃ葁���i�K�ŐU�����������Ȃ��Ă��܂��܂��B
�@�}�ł� ��x �̍��ɂ�����W���̔䗦�𑝂₷�悤�ɂ��ĕω������Ă��܂��B
�@a = 0.95, b = 0.05 �ł� x = 20 �` 25 ������܂Ŏ������̂т܂����A����ق� ��x �̍��̏d�݂𑝂��Ă� 25 < x ������Ŏ����̌������n�܂�܂��B
�@ �@