問題41 ギザの大ピラミッドがつくる影の面積 [高2★★☆☆☆]
図のように水平な地面の上に底面の1辺の長さが 2 a 、高さが b のピラミッド(四角錐) A - B C D E があり、ちょうど A B E 面が太陽に照らされているとします。地面から測った太陽の角度を θ とします。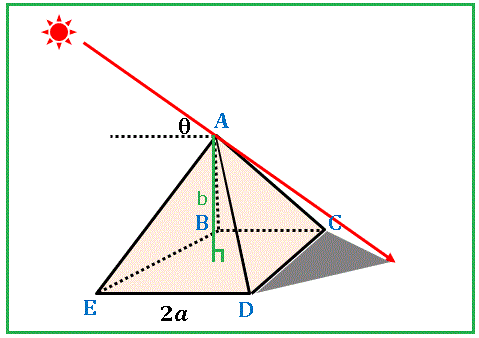
(1) ピラミッドがつくる影の面積 S(θ) を求めてください。
また、 θ のとりうる範囲も明示してください。
(2) ギザにあるクフ王のピラミッドは、底面の1辺の長さが約 230 m、高さが約 140 m あります。冬至の日の正午における太陽高度を約 37°と考えて、ピラミッドのつくる影の面積を求めてください。計算には tan37°= 0.754 を用いて、得られた数値の小数点以下を四捨五入して解答してください。
[ヒント] 三角比の基本的な知識を問う問題です。
≫ [Amazon数学書籍] 面白くて眠れなくなる数学パズル
解答41(断面図を描いてみます)
(1) 下図のように CD の中点 M をとって断面図を切り出します。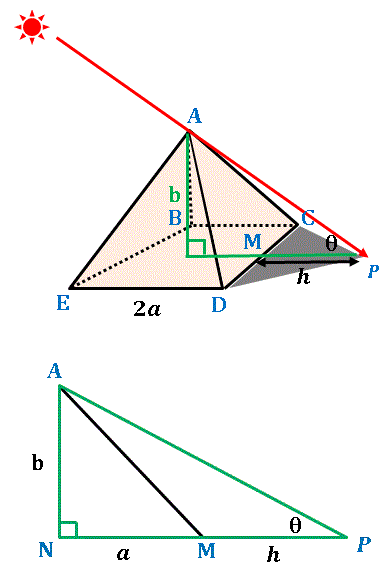
すると θ と a, b および影の高さ h との関係が
b = (a + h) tanθ
であることがわかるので
h = (b / tanθ) − a [*]
となります。影の底辺の長さは 2 a ですから、影の面積は
S = (2 a) h / 2 = a h = (a b / tanθ) − a2
となります。
次に θ の範囲を考えます。 0 < θ は明らかですが上限もあります。影が存在するには h > 0 となる必要があります(あまり太陽の高度が高いと影ができません)。そこで h = 0 となる角度を調べるために [*] の右辺を 0 とおいて
tanθ = b / a
となります。この式を満たす θ を θ = α とおけば、
0 < θ < α
が θ のとりうる範囲となります。
(2) (1) の結果に具体的な数値を入れて計算します。
a = 115, b = 140, θ = 37°ですから
S(37°) = (115・140) / tan37°− 1152 = 8127.8 = 8128 m2
が答えとなります! さすがピラミッド、影も巨大ですねー!
[補足] ちなみに冬至のときの太陽の南中高度は
90° − 北緯 − 23.4°
によって計算できます。ギザの北緯は 30°ですから、
90° − 30° − 23.4° = 36.6°
が正確な南中高度となります。気になる人はこちらの値でも計算してみてください。
無料ブログを試してみてください
「ちょっと気分が乗ったときに記事を書いて投稿する」というような感じで気軽にブログを楽しみたいというだけなら、無料ブログサービスをお勧めします。このブログは FANBLOG というサービスを使っています。他にも FC2 ブログやアメーバブログなど、色々な無料ブログがありますから、ネットの情報で使い勝手を比較しながら、お好みのサービスを選択してください。無料ブログを利用するメリットは、なんといっても「お金がかからないこと」です(当たり前です)。デメリットはやはり容量が少ないこと(500MB 〜 1GB)、カスタムできる範囲が限られていて、自分好みのレイアウトにすることが難しいこと( FC2 は例外)、無料ブログを提供する会社自身の広告が貼られていること( FANBLOG は例外)ですね。こうしたデメリットが気になる人は次回の記事を読んでみてください。