指数関数を組込んだ数列
f(1) = 1 としてf(n + 1) = exp(1 - n/10) f(n)
という数列を考えてみます。具体的に並べてみると
f(1) = 1
f(2) = exp(8/10) f(1) = exp(8/10)
f(3) = exp(7/10) f(2) = exp(15/10)
f(4) = exp(6/10) f(3) = exp(21/10)
・・・・・・・・・・・・・・・・・
という具合になります。横軸に n, 縦軸に f(n) をプロットして滑らかな曲線でつないでみましょう。
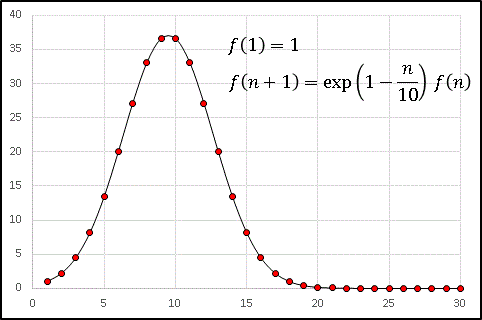
このように1つの山を作ります。n = 0 ~ 18 までは n = 9, 10 のピークを中心に左右対称になっています。 n = 19 以降は f(n) → 0 に収束します。
三角関数を組込んだ数列
次は f(1) = 1 としてf(n + 1) = cos(1 - n/10) f(n)
という数列です。エクセルでグラフを描いてみると ......

段丘のような図になっています。 n = 1 から減衰して、いったん平らになったあとまた減衰して最後は 0 に収束します。