原点から遠ざかるほど波の振幅が大きくなります
今回は m をパラメータとして、y = sin(mx)/cosx
という関数を調べてみます。
m = 1 であれば y = tanx ですね。
m = 2 のときは sin2x = 2sinx cosx より
y = 2sinx
となります。m = 3 のときは ...... 3倍角の公式を使うと、よけいにややこしい式になるので、このままにしておきましょう。それではグラフです。
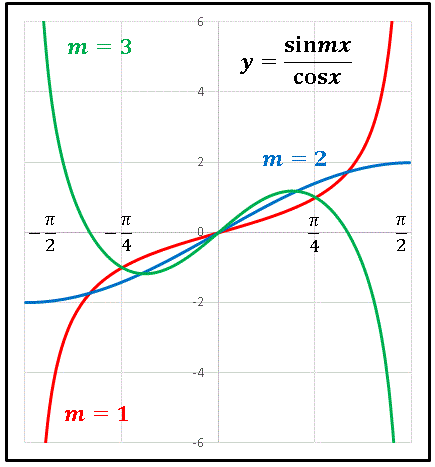
区間は −π/2 < x < π/2 に限定しています。 m = 1 のときは両端で y → ±∞ となりますが、m = 2 では ±2 という値をもちます。 m = 3 では再び両端で y → ±∞ となり、極大値と極小値が出現しています。m = 8 のグラフを描いてみると ......
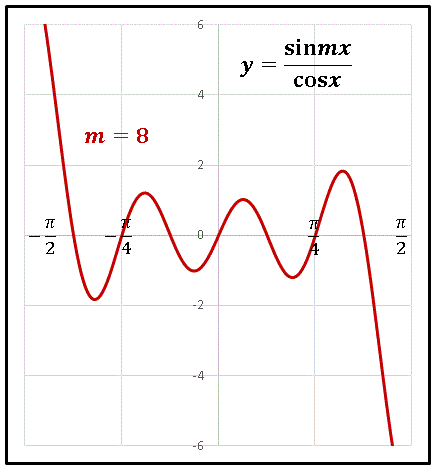
波の数が増えていますね。
さらに大きく、m = 16 としてみましょう。
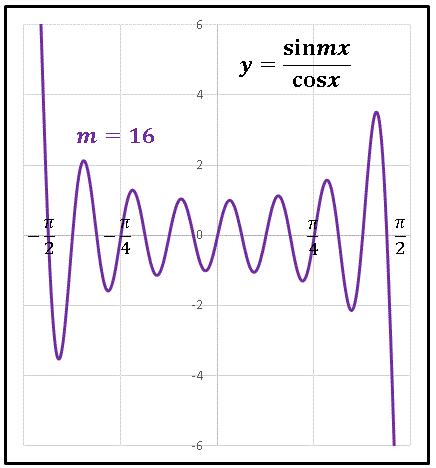
さらに振動が激しくなりました。
原点から遠ざかるほど波の振幅は大きくなっています。