原点に収斂する関数
収斂 とは、ある一定の有限確定値に限りなく近づく ということです。今はあまり使わない言葉ですが、何となく恰好いいのでタイトルにつけてみました。ようするに「収束」のことなのです。
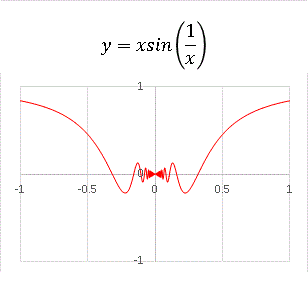
これはコンピューター数学の本でよく例に取り上げられる関数です。x = 0 では y = 0 と定義しています。 sin の中にある 1 / x は原点に近づくほど大きくなり、周期を無限に小さくしてゆくために、原点で圧縮されるような関数になります。しかし上のグラフでは原点付近の様子が見えにくいので、もう少し拡大してみます。
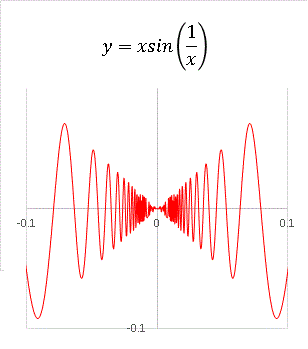
拡大してもやはり原点付近は潰されるような形になっていてよく見えません。どれだけ拡大しても同じことなのです。原点付近に波の数は無限にあるからです。もちろん、エクセルでは無限個の波を描くことはできませんから、x の刻み幅を小さくすることによって、なるべくたくさんの波を描くわけです。上のグラフで使用している刻み幅は ⊿x = 0.02 という非常に小さい値です! 次は当ブログオリジナル(かもしれない)関数です。 sin の中を 1 / log|x| としてみます。x = 0, ±1 で y = 0 と定義します。
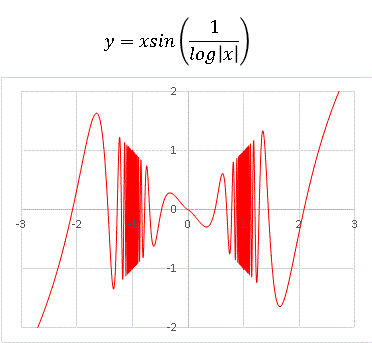
x = ±1 で sin の中が無限大になるので、その2点に圧縮されます。それにしても、とんでもない関数ですね。こういう関数はコンピューターの力を借りないと絶対に描けません。
⇒ なんとなくの数学日記(VBA は数学を学ぶのに便利です)