という式がありますね。上の式は x → 0 となる極限で sinx と x が同程度の速さで 0 に収束していくことを示しています。また、上の式が成り立つからこそ、小さな x に対して
という近似式を使うことが許されているのです。
Excel で sinx / x のグラフを描いて収束を確認します
そもそも y = sinx / x というはどのような関数なのでしょうか? グラフを描いてみましょう。
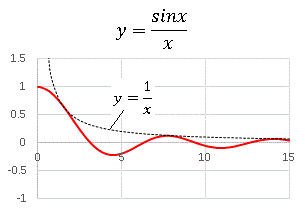
このグラフの形を予測することは難しくないと思います。 f(x) = 1 / x という関数に沿って振幅が減少していきます。今注目するのは原点付近の振る舞いなので、そこを拡大してみましょう。
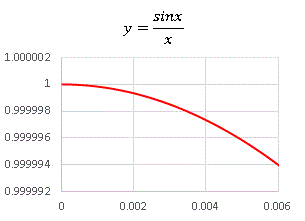
x, y ともに非常に小さな目盛をとっています。確かに x → 0 で y → 1 となっているようですね。ところで、 sinx ≒ x という近似式はどの程度の大きさの x で許されるのか気になったことはありませんか? 私はずいぶん昔に物理学の本で「振り子の角度が十分小さいときに sinx ≒ x と近似してよい」と書かれてあるのを見て、「え? 十分小さいとはどのぐらい?」と考えて電卓で確かめてみたことがありました。エクセルを使って改めて見てみることにします。そのために x と sinx の差を取って絶対値をとった y = | x−sinx | という関数を使って調べてみます。
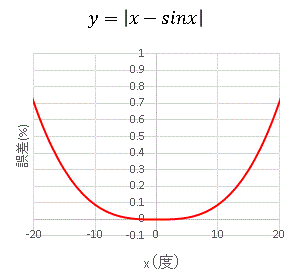
横軸は "度(degree)" の単位で、縦軸は誤差を百分率でとってあります。 x = 20°をとったとすると誤差は 0.7% 程度です。やや大きすぎる誤差かもしれません。たとえば振り子の問題で長さ L を 1m として Lsinx ≒ Lx のような計算をすると、7mm の誤差が生じてしまいます。約 1cm と考えると私としてはやはり少し躊躇しますね。 x = 10°であれば誤差は 0.1 % 未満になりますから全く問題ないでしょう。やはり x = 10°= 0.175 rad あたりまでが妥当だと思います。
最後に少し変わった関数を作ってみたので載せておきます。 sin() の中身を xsinx とした関数です。
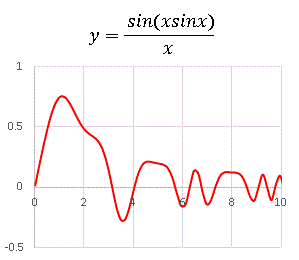
かなり複雑な形をしていますね。この関数は x → 0 のとき y → 0 となります。その理由は sin() の中の xsinx が x → 0 のとき 0×0 の形になり、結果として分子のほうが分母より速く 0 へ近づいていくからです。微積分ではこういう極限の感覚を磨いていくことが大切です。