Excel で自然対数の底 e の定義式が収束する様子を調べます
自然対数の底 e は
という関数を調べてみます。グラフを描いてみると・・・・・・
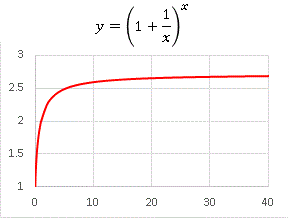
y 軸の最小値は 1 としてあります。立ち上がりが急速に、後半はのんびりと増加する関数です。当然のことながら、 x → ∞ で y → e = 2.71828 に収束していきます。
データを調べると、y の値が 2.71 を超えるのは x = 164 のときなので、x ≒ 200 ぐらいの値をとっておけば、この関数を e のそこそこの近似値として使えることになります。しかし e = 2.718 の精度を求めるのであれば、x ≒ 5000 が必要となります。
この関数の性質をもう少し詳しく考察してみましょう。 1 + 1 / x の部分は原点付近で非常に大きな値を取りますが、指数部分の小さな x がそれを抑え込むという構造になっています。指数部分の効果のほうが大きいので、結果として関数の値は小さくなります。その構図は x < 1 の範囲で続きます。x が 1 を超えると、 1 + 1 / x は x の増加とともに減少していきます。指数部分の x が値を大きくする作用は増していくので、わずかにその効きは勝ちますが、やがてそのせめぎ合いは均衡をとるようになり、それが定数 e への収束という結果に終わります。
では最後にいつものように変形バージョンを載せておきます。肩の部分を x ⇒ sinx と変形してみると・・・・・・
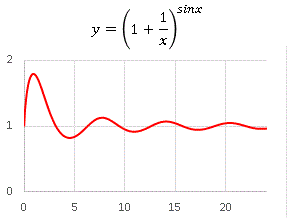
肩にある sinx は −1 から 1 の間の値しかとれないので、 x → ∞ のとき 1 + 1 / x → 1 となり、関数は揺れながらも 1 へと収束していきます。
⇒ なんとなくの数学日記(感覚を大切に)