Excel で自然対数の底 e の定義式が収束する様子を調べます
自然対数の底 e は
という関数を調べてみます。グラフを描いてみると・・・・・・
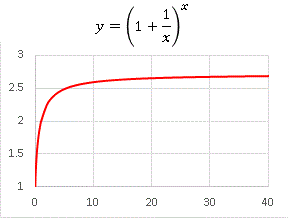
y 軸の最小値は 1 としてあります。立ち上がりが急速に、後半はのんびりと増加する関数です。当然のことながら、 x → ∞ で y → e = 2.71828 に収束していきます。
データを調べると、y の値が 2.71 を超えるのは x = 164 のときなので、x ≒ 200 ぐらいの値をとっておけば、この関数を e のそこそこの近似値として使えることになります。しかし e = 2.718 の精度を求めるのであれば、x ≒ 5000 が必要となります。
この関数の性質をもう少し詳しく考察してみましょう。 1 + 1 / x の部分は原点付近で非常に大きな値を取りますが、指数部分の小さな x がそれを抑え込むという構造になっています。指数部分の効果のほうが大きいので、結果として関数の値は小さくなります。その構図は x < 1 の範囲で続きます。x が 1 を超えると、 1 + 1 / x は x の増加とともに減少していきます。指数部分の x が値を大きくする作用は増していくので、わずかにその効きは勝ちますが、やがてそのせめぎ合いは均衡をとるようになり、それが定数 e への収束という結果に終わります。
では最後にいつものように変形バージョンを載せておきます。肩の部分を x ⇒ sinx と変形してみると・・・・・・
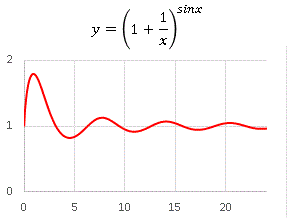
肩にある sinx は −1 から 1 の間の値しかとれないので、 x → ∞ のとき 1 + 1 / x → 1 となり、関数は揺れながらも 1 へと収束していきます。
感覚的数学?
このブログは数学的厳密さよりも感覚的なところに重点を置いています。数学科以外の一般の理数系の人にとってはこの「感覚」を磨く方が重要だと考えています。研究現場で数学的厳密さを要求されることはないと思うので。それよりも実験結果を素早くソフトで視覚化し、その意味するところを把握するスキルを身につけておくほうが大切ではないでしょうか。多くの研究現場で用いられるのは微分方程式やフーリエ変換など「解析学」に属する分野です。解析学はソフトで視覚化しやすいので、コンピューターの力を借りて「グラフを見る目」を養っておくことは決して損にならないはずです。
ただし、「今扱っている関数がどの範囲で定義されうるのか」ということだけは常日頃から注意しておいてください。エクセルを使う場合、慣れないうちは"#DIV/0!"( 0 で割ってますよ!)というようなエラーが頻発します。一見順調なようでもオートフィル機能などを使っていると、膨大なデータの中に 1 点だけエラーが混じっていた、というようなケースもあります。
まあ技術が進めば「あれ? この人、うっかりして間違ったデータを扱ってるよ。代わりに私が修正しておいてあげようっと♪」なんて言ってくれる親切なソフトも出現するかもしれませんが、今の段階では全く融通が利かないので、人間が注意するしかないのです。