Excel �ł��ɂ���ƃJ���[�p���H
�@���Ƃ��Ύ��̂悤�ȃO���t�ł��B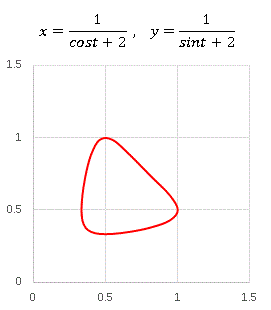
�@�}��ϐ� t �������� (x,y) �� ���ɂ��� �̂悤�Ȍ`�̋Ȑ�������邮���葱����킯�ł��B���̂��ɂ���ɗႦ��̂��Ƃ����ƁA���Ɏv�����Ȃ���������ł��B���āA���̊��������ό`����� ......
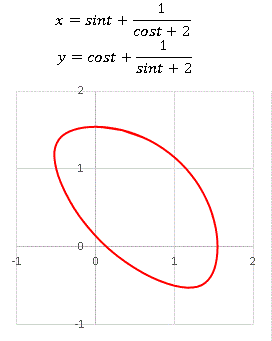
�@�J���[�p�� �̂悤�Ȍ`�̋Ȑ�������邭�铮�����ƂɂȂ�܂��B���̃J���[�p���ɗႦ��̂��Ƃ����ƁA���̍D��������ł��B���ɗg�����ẴJ���[�p���̔��������Ƃ�����u�����t�����X���������đ����ł��ł��Ȃ����v�Ǝv�����肵�Ă��܂��B���������Ď��̂悤�ȋȐ��B
�@
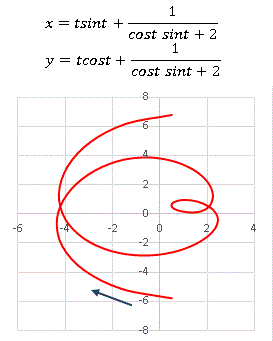
�@�|2�� < t < 2�� �͈̔͂ŕ`���Ă��܂��i pi �͉~�����j�B���_ (x, y) �͉��̕���������̕����ֈړ����܂��B����� sint �� cost �ɔ}��ϐ� t ���悶���Ă���̂ŕȐ��ɂ͂Ȃ炸�At �̑����Ƌ��Ɍ��_�ɋ߂Â��Ă����A���̂��Ɖ��������Ă����܂��B�������� t �͈̔͂��L���Ă݂܂��傤�B
�@
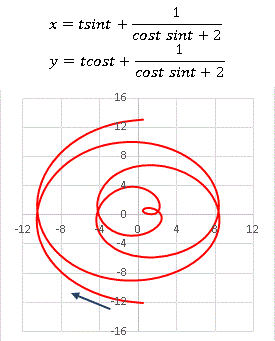
�@�͈͂́|4�� < t < 4�� �ł��B���ɉ����ċȐ��J�ɖڂŒǂ��Ă����A�O����������`���Ă��邱�Ƃ��킩��Ǝv���܂��B
�@�Ƃ���œ��_���ł����_�ɋ߂Â��Ƃ��̍��W�͂ǂ��ł��傤���H�@���ϕ��̎�@��p���Č��_����̋������ŏ��ƂȂ�_�ƁA���̍ŏ��l�����߂邱�Ƃ��s�\�ł͂Ȃ���������܂��A�������G�����Ă����Ă��̐l�͓r���Ō��ɂȂ�Ǝv���܂��B���͖ʓ|�Ȃ̂Ōv�Z����C�ɂ��Ȃ�܂���B�G�N�Z�����g���ă��N�����܂��傤�B���_�ŋߐړ_��^����}��ϐ� t �Ɠ��_���W (x, y) �A����ы��� r �́A
t = �|0.1396rad �i8deg�j
(x,y) = (0.5564, 0.3987)
r = 0.6842
(x,y) = (0.5564, 0.3987)
r = 0.6842
�ƂȂ�܂��B�����u��v�Z�ŋ��߂���I�v�Ƃ������҂�����ꂽ��A�R�����g���Ă��������B
�@
���ƂȂ��̐��w���L�@
�@�G�N�Z�����g�����Ȃ��ΐ��w�̗�����[�߂邱�Ƃɖ𗧂��܂��B�܂����̋t�ɐ��w�̕���ʂ��ăG�N�Z���̎g�������w�Ԃ��Ƃ��ł���킯�ł��B���ہA�u���W����͂��āA�G�N�Z�������g���Ēl�����߂āA�O���t��`���āA���̃O���t�����₷���悤�ɏC������v�Ƃ������ߒ���ʂ��Ă܂�ׂ�Ȃ��G�N�Z���̊�{������K�����邱�Ƃ��ł��܂��B�����ŏ��͐��w�ŃG�N�Z�����o���܂����B�@���w�Ɋւ���m����K�v���͐l�ɂ���ĈقȂ�܂����A�u�G�N�Z�����}�X�^�[����I�v�Ƃ����ړI�ł���A�Q������O�p���ŏ\���ł��B�u�܂��G�N�Z�����g�������Ƃ��Ȃ���v�Ƃ����l�́A���Ѓ`�������W���Ă݂Ă��������B������Ȃ����Ƃ�����A�R�����g�Ŏ���������������B�ł��邾�����J�ɂ��������܂��B
�@ �@