���_�Ɏ��ʂ����
�@���� �Ƃ́A������̗L���m��l�Ɍ���Ȃ��߂Â� �Ƃ������Ƃł��B���͂��܂�g��Ȃ����t�ł����A���ƂȂ����D�����̂Ń^�C�g���ɂ��Ă݂܂����B�悤����Ɂu�����v�̂��ƂȂ̂ł��B
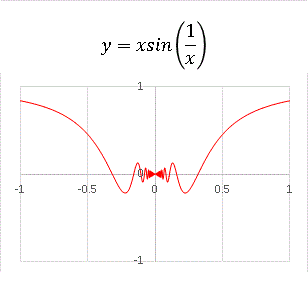
�@����̓R���s���[�^�[���w�̖{�ł悭��Ɏ��グ������ł��Bx = 0 �ł� y = 0 �ƒ�`���Ă��܂��B sin �̒��ɂ��� 1 / x �͌��_�ɋ߂Â��قǑ傫���Ȃ�A�������ɏ��������Ă䂭���߂ɁA���_�ň��k�����悤�Ȋ��ɂȂ�܂��B��������̃O���t�ł͌��_�t�߂̗l�q�������ɂ����̂ŁA���������g�債�Ă݂܂��B
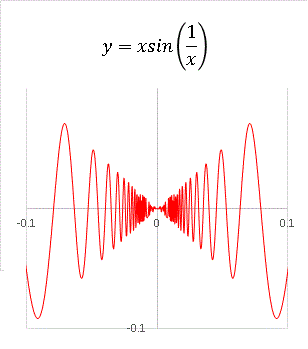
�@�g�債�Ă���͂茴�_�t�߂ׂ͒����悤�Ȍ`�ɂȂ��Ă��Ă悭�����܂���B�ǂꂾ���g�債�Ă��������ƂȂ̂ł��B���_�t�߂ɔg�̐��͖����ɂ��邩��ł��B�������A�G�N�Z���ł͖����̔g��`�����Ƃ͂ł��܂���Ax �̍��ݕ������������邱�Ƃɂ���āA�Ȃ�ׂ���������̔g��`���킯�ł��B��̃O���t�Ŏg�p���Ă��鍏�ݕ��� ��x = 0.02 �Ƃ������ɏ������l�ł��I�@���͓��u���O�I���W�i���i��������Ȃ��j���ł��B sin �̒��� 1 / log|x| �Ƃ��Ă݂܂��Bx = 0, �}1 �� y = 0 �ƒ�`���܂��B
�@
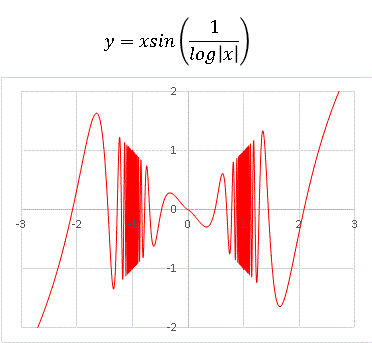
�@x = �}1 �� sin �̒���������ɂȂ�̂ŁA���̂Q�_�Ɉ��k����܂��B����ɂ��Ă��A�Ƃ�ł��Ȃ����ł��ˁB�����������̓R���s���[�^�[�̗͂���Ȃ��Ɛ�ɕ`���܂���B
�@
VBA �͐��w���w�Ԃ̂ɕ֗��ł�
�@VBA �͂��̉��l���Ⴍ����ꂪ���ł����A�g�����Ȃ���悤�ɂȂ�Ζ{���ɐF�X�Ȃ��Ƃ��ł���悤�ɂȂ�܂��B���� Excel �𐧌�ł���Ƃ����_���A���̃v���O���~���O����ɂ͂Ȃ����݂ł��B�������A����͓��ɐ��w�������Ƃ��ɂ���ϕ֗��ŁA�u������ɂ��ĕ����̕ϐ������Ȃ���O���t�͂���v�Ƃ����悤�ȖړI��B����܂łɗv���鎞�Ԃ̓G�N�Z���E VBA ���ő����Ǝv���܂��B���̃v���O���~���O����ł��������Ƃ͂ł��܂����A���Ȃ�̎��Ԃ��₷���ƂɂȂ�܂��B���̃u���O�ł������� VBA ���g�������͂��Љ�����ł��B�@ �@