こばとの数学基礎講座 16 ネイピア数と自然対数
円周率と並んで数学で最も大切な定数がネイピア数(Napier's number)"e" です。発見者であるスコットランドの数学者 ネイピア(John Napier) にちなんだ呼び名です。ネイピア数は無理数でe = 2.718281828 ・・・・・・
という値をもっています。 e はとても不思議な数です。 e を底とする指数関数
y = e x
という曲線を考えたとき、曲線上の任意の点における接線の傾きがこれまた
m = e x
という形で表されます:
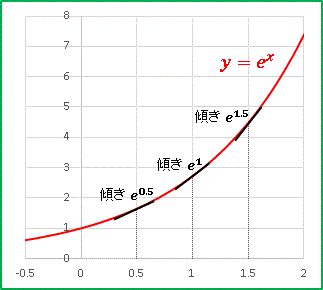
当ブログでは y = e x のことを
y = exp(x)
と表記する場合もあります。exp は exponential(指数関数)の略です。
y = ex の逆関数である
y = logex
のことを自然対数(natural logarithm)と呼びます。多くの数学書と同様に、当ブログでも自然対数の場合に限って底の表記を省略して簡単に
y = logx
と書くことにします。ただ、本によっては自然対数を
y = lnx
と表記して、底を 10 とする常用対数のことを y = logx としている場合もあるので注意してくださいね(たいていは本の最初の方に記述ルールに関して触れてあるはずです)。
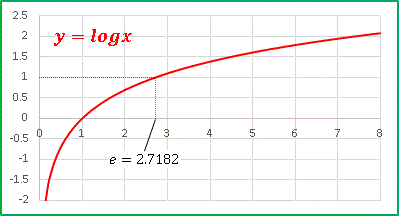
さて今回からいよいよ「正確な対数値」を求める作業に踏み込んでいきます。その土台となるのが「素数の自然対数」なのです。sinx や cosx, 或いは logx のような連続関数は x の級数の形で表すことが可能であることが知られています。その表式を得るための手順は高校数学の範囲を超えるため省略しますが、表式自体は簡単です。まずは log2 を得るためにたった1回だけ
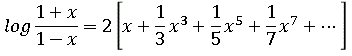
という式を使います。 x = 1/3 のきに左辺が log2 となることを確認してください。右辺は単調で面倒な計算をひたすら行って(皆さんは計算しなくていいですよ)、
log2 = 0.69315
という高い精度の値が得られます。そして log3 以降は次式を繰返し使うことになります:
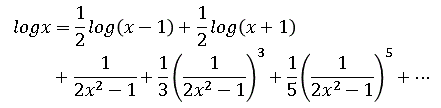
上式から素数の自然対数を次々に得ていきます:
log3 = 1.09861
log5 = 1.60944
log7 = 1.94591
log11 = 2.39790
log13 = 2.56495
log17 = 2.83321
・・・・・・・・・
log5 = 1.60944
log7 = 1.94591
log11 = 2.39790
log13 = 2.56495
log17 = 2.83321
・・・・・・・・・
こうして得られた素数の自然対数を用いれば、前回学んだ公式を用いて合成数の自然対数を求めることができます。たとえば
log10 = log(2×5) = log2 + log5 = 2.30259
というように計算できるわけです。これで前回の宿題として残された
log2100 = 2 + 2log25
が計算できそうな気もしますが、残念ながらまだです。よく見てください。求めたいのは
log25
の値です。底が違っています。そこで次回では「底の変換公式」を学びます。特に次回はおそらくどの本にも載っていないようなびっくりするような手法で公式を解説しますよ! お楽しみに!