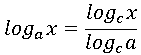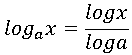こばとの数学基礎講座 17 底の変換公式の意味をグラフを使って考えます
前回学んだように素数の自然対数のリストが用意されたなら、それを元にしてあらゆる対数の計算が可能となります。特に要となる計算技術が 底の変換公式 です。次のように底 a, 真数 x の対数を底 c の対数で表すことを考えます:y = loga x ⇒ logc x の形を含む式
導出は簡単です。y = loga x を
x = ay
の形に直して c を底とする対数をとります:
logc x = logc ay
前々回に学んだ
logaR t = t loga R
という公式を用いて右辺を変形します:
loga x = ylogc a
y = logax ですから
loga x = loga x logc a
となって、
という公式が得られます。c が自然対数 e の場合は、前回取り決めたように底の表示を省略できますから、
となりますね。これでようやく前回までの宿題として残されていた
log2 100 = 2 + 2log2 5
を計算することができますね。まず log2 5 の底を e に変換します:
log2 5 = log5 / log2
ここで前回に計算した素数の自然対数値
log2 = 0.69315
log5 = 1.60944
log5 = 1.60944
を用いて計算すると
log2 5 = 2.32192
となります。したがって
log2 100 = 2 + 2 × 2.32192 = 6.64384
という値が得られますよ! ちなみにエクセルでより正確な値を求めてみると、
log2 100 = 6.64385619
ですから、小数点以下3桁までの精度で計算できたことになります。この計算精度は前回に載せた自然対数の級数展開で何項まで計算するかで決まります。ちなみにエクセルのような表計算ソフトも内部では級数を使って関数を計算しています。しかし昔の人は電卓すらなかったわけですから、コツコツと手計算で膨大な計算をして対数表を作っていたのです。本当に頭が下がる思いですね。
さてここからは底の変換公式のもつ意味を視覚的に解説していきます。
2通りの方法で説明を試みます。
まず最初に底が 2 と 10 である2つの対数関数
y = log2 x
y = log10 x
y = log10 x
のグラフを描いてみます:

1 < x の範囲では log2x が log10x の上にきます。直感的にわかる人もいると思いますが復習も兼ねて一応確認しておきます。たとえば x = 10 という値で考えたときに、
log2 10 = "2k = 10 の解 k (k > 3)"
log10 10 = "10k = 10 の解 k (k = 1)"
log10 10 = "10k = 10 の解 k (k = 1)"
となりますね。明らかに
log2 10 > log10 10
となります。そこで log2 x の底を 10 に変換することを考えてみます:
log2x = log10 x / log10 2
となりますね。ここで右辺の
1 / log10 2 = 3.32193
という数は log2 x と log10 x の比率を表しているのです。しかもその比は真数 x がどういう値をとっても一定です。言い換えるなら、「 log2x をどうしても log10 x を含む形で表したいのであれば、係数 3.32193 という値を掛けて調整しなければなりませんよ」ということなのです:
log2 x = 3.32193 log10 x
それでは2つめの方法で説明してみます。こちらはたった1つのグラフでより本質的な見方ができます。用いる関数は普通の対数関数ではなく、真数を固定して底を変数とする
y = logx 10
という関数です! 普段はあまり見ることのない形ですね。指数形式に直すと
xy = 10
という関係ですが、やはりこんな表式はほとんど見る機会はないと思います。とりあえずグラフを描いてみましょう。
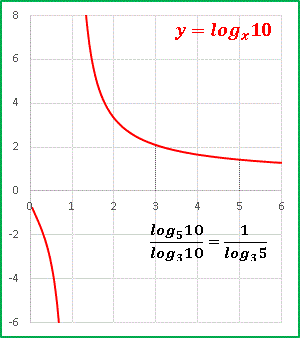
今は 1 < x の範囲で説明します。x = 1 付近から急激に値を減らしていきますが、x が大きくなるにしたがってその減少率は緩やかになっていきます。このグラフは「真数 10 について、底が増加したときその対数値はどうなっていくのか」ということを明確に表しています。そこでたとえばこのグラフ上の2点
(x, y) = (3, log3 10)
(x, y) = (5, log5 10)
(x, y) = (5, log5 10)
を抜き出して比較したとき、その減少率は底の変換公式における係数になっているはずですね。つまり log510 を log310 を含む形で表したいのなら、 log310 は大きすぎるので
log5 10 = log3 10 / log3 5 = 0.683 log3 10
という変換で log3 10 に係数を乗じて値を減少させなければならないということです。
本日はここまでです! それではまた次回お会いしましょう!
(暇があるなら、こばとの雑談を読んで帰ってくださいな)
こばとの雑談
前回、向こうの世界ではネイピア数 e のことを "コンダ" と呼ぶとお話しましたね。今回は e0 や e1 の呼び方です。
0 はエン・エラカダ語(古エラカダ語)で "エン" と発音します。
"エン" は「無」や「真空」を第1義としますが、
「不動、永遠、太古」という意味もあります。
e0 は "エン・コンダ" と言います。
底が e の場合に限って「〜乗」を意味する "ク" を省略できるのです。
1 は "ヴィ" なので e1 は "ヴィ・コンダ" 、
2 は "パズ" だから e2 は "パズ・コンダ" 。
未知数 x に相当するエラカダ語は "チェカ" です。
なので ex は "チェカ・コンダ" となります。
まあでも、こちらの世界とあちらの世界、書き方・読み方が違っても数学の本質的な部分は全く同じですね。数学は自然界を表記する手段ですから、世界が異なっていても物理法則が同じならば必然的に数学もまた同一のものとなってしまうのは当たり前なことなのかもしれませんけどね。
物理法則と言えば、その昔、姉は古風な手段を使って一生懸命に万有引力定数や電子のもつ電荷などを調べたことがあるそうです。「観測できる範囲内で数値は全く同じ。びっくりした」とは姉の言葉。「もしかして同じ宇宙の遠い惑星に来てしまったのかと錯覚しそうだった」とも言っていました。こばとは物理学に関してはそれほど詳しくないのでなんともいえないのですが、不思議なこともあるものですね。
(注:エン・エラカダ語のカタカナ語表記はかなり適当です。"エン" は "イェン"、"パズ" は "プァズ" と表記したほうがまだ原音に近いかもしれませんが、そもそもカタカナ語で表すこと自体にかなり無理があります。そして何より私自身のエラカダ語の発音がとーっても怪しいのです。母国語のスカヴア語は姉にみっちり仕込まれましたけど、エラカダ語はこばとたちにとっても完全に外国語です。数学・科学用語は借用されていましたけど、それはつまりスカヴア語風に発音されてしまうわけです。いや、そもそもエン・エラカダ語は古い時代のエラカダ語だから、現代エラカダ語とは発音がだいぶ変わっているだろうし・・・・・・こんなややこしいことをつらつら書いても誰も読んでいないかもしれませんね。もうこのへんでやめとこうっと)