こばとの数学基礎講座
三角関数とベクトル編⑧ 平面上でベクトルをつなぎ合わせます
ベクトル使ってて面白いのは、やっぱりつなぎ合わせねー。つまり足し算ねー。前に数直線上でやったことを、今度は平面上でやってみましょー。まずは座標 (1, 1) まで矢印を引いてみますよー。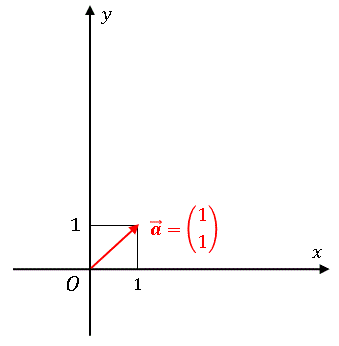
このベクトルを
と書きましょー。今度はこの矢印の先に
をつないでみましょー。
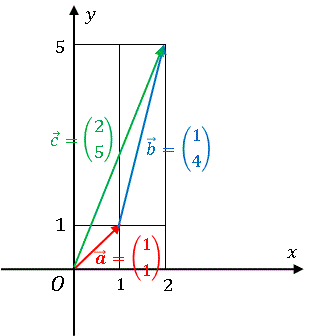
こんなふうになりますねー♪ 愉快ねー♪
青と赤のベクトルを足して、緑のベクトルになったと考えるのです。
これは x, y 方向にそれぞれ 1 と 4 を加えるという操作ですから、
というような演算をベクトルの足し算ということにします。これは数直線上のベクトルの足し算を自然な形で拡張していますよ。上の式を変形すると
となります。つまり
です。このような形でベクトルの引き算も定義することができるのです。
ところで座標 (2, 5) まで行く経路は他にも無数にあります。とにかく目的地にたどり着けるようにベクトルをつなぎ合わせればいいのです。たとえば下の図のように、あちこち寄り道したっていいのです。

これを成分表示で書くと
となりますよ。数直線上の足し算に比べるとずっと自由度が高いのです。面白いですねー。皆さんもあれこれつなぎ合わせて遊んでみてねー。 ≫ 三角関数の具体的な値