こばと、小さな出版社を経営してるんだけど、どうも実感ないのねー。それどころか、人手不足の影響だけは、もろに受けて、アルバイトの求人さえままならない状況なのねー。なんかもっと、どかんと売れるベストセラーを出版して、○学館とか、△談社みたいに大きな出版社になりたいのねー。『こばとちゃんの Excel 体操』なんてどうかな? え? そんなの売れるわけない? そうですかねー。あ、それからねー、お世話になっている印刷会社の逆井さん、来年ついに定年を迎えるそうです。ついこの前知り合ったような気がするのに、時が経つのは早いものですねー。え? いい加減おしゃべりはやめて本題に入れ? はいはい。それでは数学講座を始めましょー。
こばとの数学基礎講座
三角関数とベクトル編⑩ ベクトルの大きさを計算しましょう
下の図のように、原点 O と座標 (2, 3) を結ぶベクトル
の大きさ
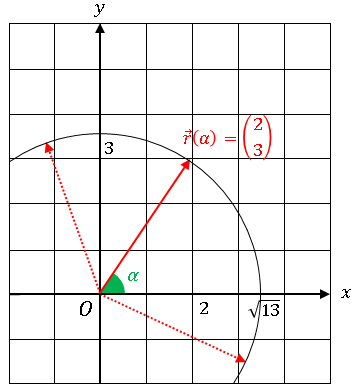
これは簡単ねー。三平方の定理を使って
となりますねー。一般に
の大きさは
と計算できますよ。さて、以前にも単位円で同じようなことを話しましたけど、上の図にあるように、大きさ
と表すことができます。
と書くことができます。このように、角度と大きさを使う表式を「極形式」とよびます。もちろん、たとえば
のようなベクトルであれば、θ = π/4 であることがすぐにわかるので、
と表すことができます。 ≫ ベクトルの内積