�@�����͓��ςɂ��Ęb���܂��B�����ł����A�F����B
�@�x�N�g���̓��ρA����͂ƂĂ���Ȃ��Ƃł��B
�@���͉��̂��߂ɂ���Ȃ��Ƃ��w�Ԃ̂��Ǝv����������܂���B�����������A�����N�������v�Z�̓r���œ��ɖ�������A�ǂ������ς̂��Ƃ�U��Ԃ��Ă������� ...... ���̃l�^�A�Ⴂ�l�͒m��Ȃ���ˁB�������������Ă����ƁA�����搶�ˁ`�B
�@���a�̍��A���Ƃ����T���������M�S�Ɍ��Ă����ǁA���v���Ԃ��ƁA���Ȃ�Ԃ��Ƃb�ˁ[�B�F������@������ DVD ���ĊςĂˁ[�B���ł� Amazon �̐�`���Ă��������ƁB
 | 3�NB�g�����搶 ��1�V���[�Y �������BOX�Z�b�g [DVD] ���É��i |
���Ƃ̐��w��b�u��
�@�O�p���ƃx�N�g���҇J�@�]���藝�ƃx�N�g���̓���
�@�Ƃ����킯�Ŗ{���� �x�N�g���̓��� �̂��b�ł���`�B
�@�܂��͉��̐}�����Ă��������ȁ`�B
�@
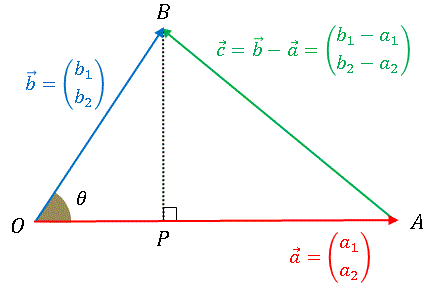
�@O ���n�_�� A �� B �܂ň������x�N�g�������ꂼ��
�Ƃ��܂��傤�BA ���� B �Ɉ������x�N�g����
�ƂȂ�܂��BB ���� OA �ɐ��������낵�Č�_�� P �Ƃ��܂��B������ AB �̒����� OA �� OB �ŕ\�����Ƃ��l���܂��B�O�����̒藝���g����
�ƂȂ�܂��B�����Ńx�N�g���ƎO�p����p�����
�ƕ\�����Ƃ��ł���̂�
�@�����ŎO�p���Ɋւ����{����
��p�����
�ƂȂ�܂��B����� �]���藝 �Ƃ�т܂��B�����ĉE�ӂɌ��ꂽ
�� �x�N�g���̓��� �ƒ�`����
�Ƃ����L���ŕ\�����Ƃɂ��܂��B����Ɨ]���藝��
�Ə������Ƃ��ł��܂��B���x�́A���̗]���藝���x�N�g�������ŕ\���Ă݂܂��B
�Ȃ̂ŁA�O�����̒藝��p����ƁA�x�N�g���̑傫���̕����͂��ꂼ��
�ƂȂ�܂��B�����]���藝�ɓ���Đ��������
�Ɛ����ŕ\�����Ƃ��ł��܂����B
�x�N�g���̓��ς̈Ӗ�
�@���炽�߂Ē�`�����������茩�Ă݂�ƁA���ς͐}�̂悤�Ƀx�N�g��
�@
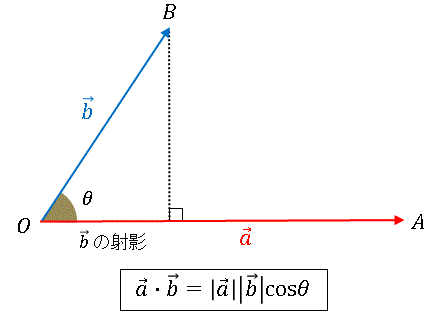
�@�����Œ������W�� x ���ɉ�����
�@
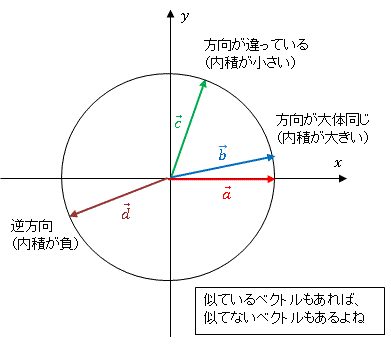
�@���ς̒l�� cos�� �ɂ���Ă���̂ŁA���Ƃ��Α� 1 �ی��ł� �� ���傫���Ȃ�قǓ��ς͏������Ȃ�܂��B�܂�
�@�܂���ςƂ́u���݂��������悤�ȕ����������Ă��邩�ǂ����v�A�u���Ă��邩�ǂ����v�Ƃ����ڈ��ɂȂ�̂ł��B���̃C���[�W�͂ƂĂ���ŁA���͊����܂������̐��������x�N�g���ƍl���邱�Ƃ��ł��āA�قȂ�����m�̓��ς��Ƃ��Ă݂�Ɓu���݂������Ă��邩�ǂ����v�Ƃ������Ƃׂ邱�Ƃ��ł���̂ł��B
�@�����l�ԊW�ł��Ƃ���ƁA��≿�l�ς����Ă���ғ��m�͒��ǂ��Ȃ��Ęb������オ�邯�ǁ`�A�����̍l����������i���̓��ς����j�l���m���ƁA�����ꐶ�����肠���Ȃ����Ă��ˁ`�B���H�@�ςȂ��Ƃ��H�@�����ł����ˁH�@����͓��ςƒ��p�ɂ��Ă��b���܂���`�B�܂��ˁ`�B
�@�@≫ 2 �̃x�N�g�������p�Ȃ�Γ��ς� 0 �ł���`
�@
�@