え? そのネタは前にもやった? そうだっけ?
あ、そうそう、金八先生ごっこなんてやってる場合じゃないんですよ~(←じゃあ、やるな)。ま、いいや。とにかく講義を始めましょ~。
こばとの数学基礎講座
三角関数とベクトル編⑫ 2 つのベクトルが直角ならば内積は 0 です
前回に引き続いて内積のお話です。内積はというように定義されていましたね。ここで θ を 0 にすると、内積も 0 になってしまいます。
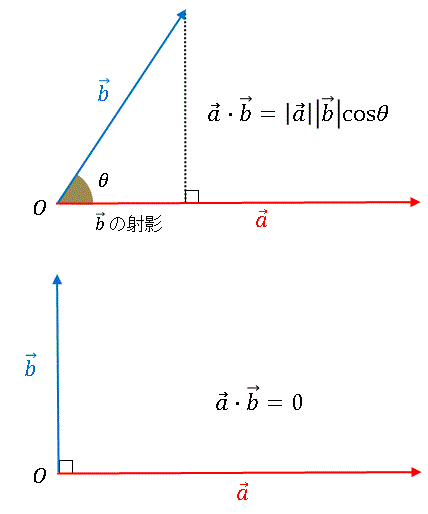
この性質は数学の色々なところで使われているし、大学入試問題でも頻出するので、受験生は「直角」と言われたら「内積 0 !」と条件反射で叫んでしまうぐらいになじんでおかないとダメですよ。まあ、本当に叫んだら、ただの変な人だけどね。さて、内積を成分表示すると
と表されることをすでに学んでいます。そこでどう考えても明らかに直角なベクトル
について公式を確認してみますよ。

ちなみに、このように長さ 1 のベクトルのことを単位ベクトルとよびます。内積をとってみましょ~。
確かに 0 になりましたねー!
この 2 つのベクトルは紛れもなく直角です!
え? そんなことわかりきってる? あ、そう。
それでは今度は逆に、あるベクトル
が与えられたとして、これと大きさが同じで直角なベクトル
となります。右辺を 0 にすればいいのですから、
としてやればいいのです。でも、
としても、やっぱり内積は 0 になりますね~。このベクトルをあらためて
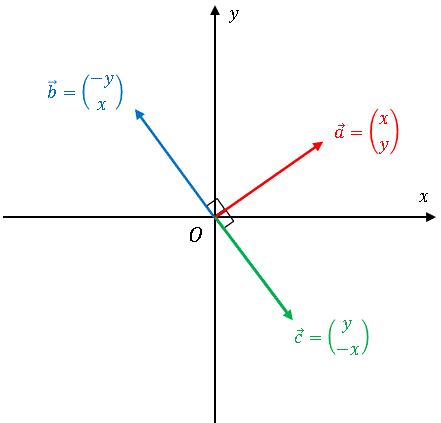
図を見れば、適当な平面ベクトルと同じ大きさで直交するベクトルは 2 本あることは一目瞭然です。その 2 本は互いに逆向きになっています。つまり、これらの内積は -|a|2 になっているはずです。確かめてみましょ~。
ちゃんと -|a|2 になっていますね。まあともかく、こんなふうに、ベクトルの内積は角度の情報を与えてくれるので、なにかと便利なのです。みなさんもどんどん内積をとってくださいな~。それではまた次回お会いしましょ~。
≫ 次回は加法定理を導きますよ♪