数学問題のほうは、姉妹サイト『 Excel VBA 数学教室』のほうで定期掲載を続けますので、そちらもよろしくお願いします。
微分して周期の近似値を求めます
さて今回扱うのはf(x) = exp(cosx) logx
という関数です。指数関数、三角関数、対数関数が揃い踏みの豪華な関数ですよ。
g(x) = logx, h(x) = exp(cosx)
も一緒に Excel でグラフを描いてみましょう。
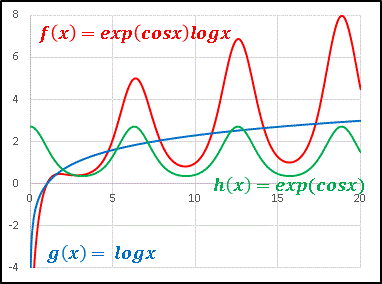
h(x) は周期 2πの振幅を変えない周期関数です。そこに緩やかながらも増加関数である g(x) をかけると、振幅を増加させる周期関数 f(x) が得られます。グラフではちょっと見えにくいかもしれませんが、 h(x) と f(x) の周期はほんの僅かにずれています(特に一番左端の山の部分をよく観察してみてください)。 f(x) を微分して確認してみましょう。
f'(x) = exp(cosx) [1 / x - sinx]
f' = 0 とおくと、 exp(cosx) > 0 ですから、
1 / x - sinx = 0
という極値を求める式が得られます。この式の解を求めるのは容易ではありませんが、x が十分に大きいところでは 1 / x は無視できますから、近似的に
sinx = 0
とすることができて、その周期が約 2πであることがわかります。上のグラフでも、 3 つめの山になるとずれが判明できないほど周期が一致していますね。
⇒ 円周率の表記について