アステロイドに収束する曲線
今回はアステロイドの方程式にベッセル関数 Jn を組み込んでみます。ベッセル関数は減衰振動関数です。詳しい解説はこちらを参照してください。
まず最初に
x = [J0(θ) + cosθ]3
y = [J0(θ) + sinθ]3
y = [J0(θ) + sinθ]3
という方程式の様子を見ます:

-4π ≦ θ ≦ 4πの範囲で描いています。ベッセル関数は原点付近にピークを持ち、|θ| の増加にともなって減衰していく関数なので、 θ ≪ 0 (θ がとても小さいところ)では動点 (x, y) は図の内側に描かれたアステロイドに近い軌道を描きます。θ が 0 に近づくとベッセル関数の影響が大きく現れるので外側の大きな軌道へ移ることになります。そのあとまたθの増加とともに内側 へ入り込んでいき、θ ≫ 0 (θがとても大きいところ)ではまたアステロイド付近をぐるぐる回ることになります。
基本はこの形ですが、 Jn の number を変えていくとより複雑な軌道を描くようになります。まとめて掲載しておきます。

いずれも |θ| ≫ 0 ではアステロイドに収束する曲線です。
最後におまけとして
x = [J1(θ) + cosθ + cos(θ/2)]3
y = [J0(θ) + sinθ + cos(θ/2)]3
y = [J0(θ) + sinθ + cos(θ/2)]3
という方程式のグラフを描いてみます:
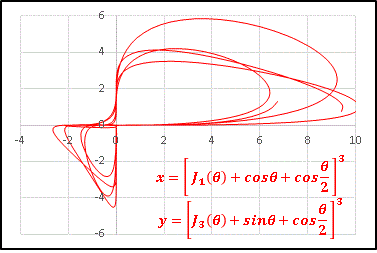
もはやアステロイドとは関係ありませんが、媒介変数表示関数の描く模様はいまだに全く予測できませんね。
⇒ 数学の歴史