Excel で鮫の歯のようなグラフを描きます
何となく Excel をいじっていたらこんな面白いグラフを発見しました。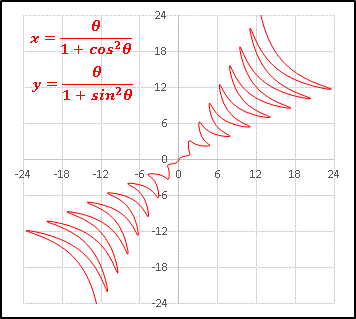
鋭い歯のような形 が並んでいますね。
この方程式をベースに色々と試してみると次から次へと変なグラフが出現しました。
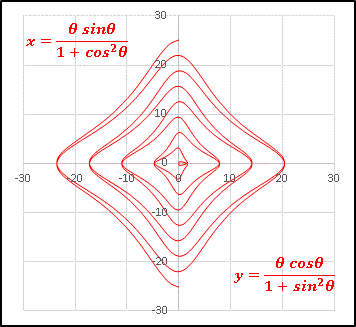
分子に sinθ と cos θ を掛けています。
歪んだ菱形が連なったような形ですね。
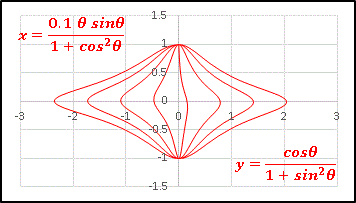
y の分母から θ を取り去って、横スケールを調整するために x を 1/10 に縮めています。
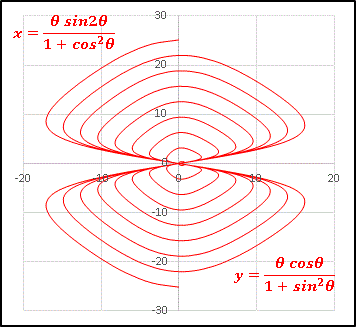
開いた貝殻のような形? 上手く表現できませんね。
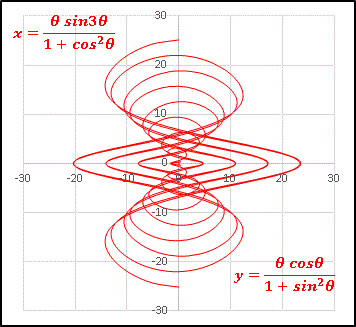
とても複雑な軌跡ですが、対称性は保たれていて美しいですね。
sin の中の θ を少し変えるだけでグラフの形はどんどん変わります。
皆さんもあれこれと試してみてください。
⇒理系英単語 15