Excel で変幻自在のグラフを描きます
三角関数を含んだ媒介変数方程式x = t(cost + sin2t), y = t(sinat + cos2t)
において a を変化させていきます。今回は細かい解説抜きでコンピューターの描き出す変幻自在のグラフを眺めて楽しんでください。

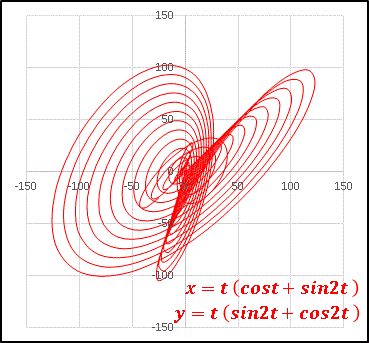
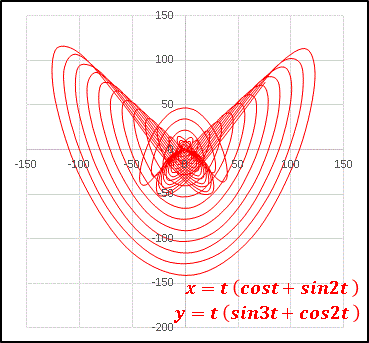
いかがでした? sin の変数を少し変えるだけでこれほど複雑に様相を変化させるのです。媒介変数表示の方程式は y = f(x) の形に表せないものがほとんどで、とても複雑な曲線を描きます。関数の組合せは無数にあると思うので、まだまだ知られていない形がたくさんあると思います。皆さんも「こんなグラフを見つけたよ!」というものがあれば、コメントで教えていただけると嬉しいです。
⇒ なんとなくの数学日記