�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
�L��
�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
posted by fanblog
2024�N10��28��
�w�N���ʂƐ��тɊW�͂���̂��H�@���ʑw�̏ꍇ
�ŋ߂͊w�N���ʂ��o�Ȃ����w�Z������ƕ����܂����A���̊w�Z�͏o�܂��B�P�ʁ`�r���܂ŃK�b�c���B
���ʂ͒���e�X�g���ƂɂT���Ȃ̍��v�_�ł��B
���v450�_�ȏ���悤�ȃg�b�v�w�͐��т��ق�5�ł��傤�B
�������A�w�N���ʂ����ʑw�̏ꍇ�͐��тɌ��\��������悤�Ɏv���̂ł��B
����́A���ʑw�̊w�N���ʂƁA���т̊W�ɂ��čl���Ă݂����Ǝv���܂��B
�����ǂ������u�܁A���ϓ_������^���Ă��ƂŁB�����܂ň����Ȃ��B�v
������Ė{���ł��傤���H
���ϓ_�ƕ����ƁA���������^�̏��ʂ��Ǝv�������ł���ˁB�������A�Ⴄ�̂ł��B
���̊w�Z�ł́A����e�X�g�̂��тɓ��_���z���z���܂��B
�e���Ȃ��ƂƁA5���Ȃ̍��v�_�œ��_���z���o��̂ł����A10�_�P�ʂŐl�����z���킩��悤�ɂȂ��Ă��܂��B
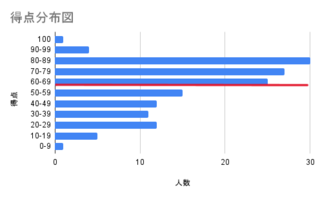
�ȉ��ɃT���v���̕��z�}���ڂ��܂����B�ԃ��C���͕��ϓ_�Ƃ��܂��B
������A���ϓ_��61�_�Őԃ��C���ɂȂ�܂��B�ł��A��Ԑl���������̂�80�`89�_�͈̔́A�Q�Ԗڂɐl���������̂�70�`79�_�͈̔͂Ȃ̂��킩��Ǝv���܂��B
���̏ꍇ�A�����̓_�������ϓ_�ł����Ă��A���ʂł����Ɛ^�������ɂȂ��Ă��܂��̂ł��B
�Ȃ�Ȃ����ϓ_���10�_�ȏ㍂���_������Ă��A���ʂ͏�ʂł͂Ȃ��̂ł��B


���ʂ��オ�����A���������ň���J���Ă������P�B���鎞�����C���t���܂��B
�u���������ʂ��Ⴂ�q���A�������S�R���т��ǂ����ǁA�ǂ��������ƁH�v
�悭�C���t�����A����B
�����A���ʂ͂T���ȍ��v�_�ŏo��̂ɑ��āA���т͋��ȕʂɏo���̂ł��B
�Ⴆ���v300�_�̏ꍇ���l���Ă݂܂��B
�@�@�T���ȑS��60�_�̎q
�A�@1����80�_�A4����55�_
�B�@�Q����90�_�A�R����40�_
��L�R�Ƃ����v300�_�Ȃ̂ŁA�w�N���ʂ͓����ɂȂ�܂��B
�����A���ꂪ���тɂȂ��
�@�@�I�[��3
�A�@4���P�A3���S��
�B�@�T���Q�A�R��3��
�ɂȂ�\���������B
�������ʂȂ̂ɁA�B�̐l���_���g�c�Ő��т��ǂ��̂ł��B
����́A���т́u�R�v�����̂������L���_���܂ł��J�o�[�����Ƃ������Ƃ������ł��B
�������w���ɂȂ�A���т��T�i�K�ɂȂ��Ă킩�������Ƃ́A�u3�v�͂��̂������L���_���܂ŃJ�o�[�����A�Ƃ������ƁB
���ϓ_��葽�������Ă��u3�v����͐l�����z�}���猩�Ă��A�܂��Ó��B�������A���ϓ_���猋�\�Ⴍ�Ă��A��ۓI�ɂ͕��ϓ_��60�_�̏ꍇ�A20�_�キ�炢�܂Łu3�v�Ȃ̂ł��B
�u3�v�̒��ɂ��A3.0�`3.9�܂ŕ��z������A3.0�̐l��3.9�̐l�͒���e�X�g�Ŕ{�ȏ�_���Ⴄ�̂ɁA�������тɂȂ��Ă��܂��̂ł��B
�Ȃ̂ŕ��ϓ_�������������_�����̂����ѓI�ɂ͂P�Ԃ��������Ȃ��B
�������́A��o���A���Ƒԓx�Ȃǂ͖��Ȃ��̏ꍇ�ł��B


���Ƌ��c�������ʁA���P�ł̊w�N���ʂƐ��сA���̓��ӁE�s���ӂ��l���A���Q�������e�X�g���𐬐т��グ������֕ύX�������܂����B
���ȋ��Ȃ́u3�v������Ηǂ��Ƃ��A�����Ԃ����������ɂ���B
���̑��蓾�ӂȋ��Ȃɕ����Ԃ����āA�ł��邾���ǂ��_������Đ��т��グ��A�Ƃ������ł��B
�������ʂ��������Ă��C�ɂ��Ȃ��B���\�͐��тȂ̂ŁA���ʂɂ������K�v�͂Ȃ��̂ł��B
�Ƃ͌����A���܂���s���Ӌ��Ȃ�����Ă����킯�ɂ͂����Ȃ����R�������܂��B
����́A�����͂T���ȍ��v�_�ŃW���b�W��������ƁB
���т��グ������փV�t�g���A�e�X�g���ł͕s���Ӌ��Ȃɗ͂���ꂷ���Ȃ��A�Ƃ������ł��悤�ɂ��Ă���̂ł����A�Ƃ͌����s���Ӌ��Ȃ����Ă����Ȃ��Ȃ�͍���B
�����ł͕s���Ӌ��Ȃ��K�v������B
���̉��~���ƂĂ�����I
���̏ꍇ�A�s���Ӌ��Ȃ͂���Ă��ł��Ȃ������ɁA���Ȃ��ƑS���o���Ȃ��Ȃ��̂ł��B
�������s���Ӌ��Ȃ��P���Ȓ��x�Ȃ�Ηǂ����A���̏ꍇ�R���ȁi���E���E�Ёj������B�����ȏオ�s���ӂȂ�A���͂�����̂��̂��s���ӂȂ̂ł��A�Ƃ����C���炵�Ă���̂ł��B


���ʂ͒���e�X�g���ƂɂT���Ȃ̍��v�_�ł��B
���v450�_�ȏ���悤�ȃg�b�v�w�͐��т��ق�5�ł��傤�B
�������A�w�N���ʂ����ʑw�̏ꍇ�͐��тɌ��\��������悤�Ɏv���̂ł��B
����́A���ʑw�̊w�N���ʂƁA���т̊W�ɂ��čl���Ă݂����Ǝv���܂��B
���ϓ_��������ꍇ�A���ʂ͐^�������ɂȂ邱�Ƃ�����
�����ǂ������u�܁A���ϓ_������^���Ă��ƂŁB�����܂ň����Ȃ��B�v
������Ė{���ł��傤���H
���ϓ_�ƕ����ƁA���������^�̏��ʂ��Ǝv�������ł���ˁB�������A�Ⴄ�̂ł��B
���̊w�Z�ł́A����e�X�g�̂��тɓ��_���z���z���܂��B
�e���Ȃ��ƂƁA5���Ȃ̍��v�_�œ��_���z���o��̂ł����A10�_�P�ʂŐl�����z���킩��悤�ɂȂ��Ă��܂��B
�ȉ��ɃT���v���̕��z�}���ڂ��܂����B�ԃ��C���͕��ϓ_�Ƃ��܂��B
������A���ϓ_��61�_�Őԃ��C���ɂȂ�܂��B�ł��A��Ԑl���������̂�80�`89�_�͈̔́A�Q�Ԗڂɐl���������̂�70�`79�_�͈̔͂Ȃ̂��킩��Ǝv���܂��B
���̏ꍇ�A�����̓_�������ϓ_�ł����Ă��A���ʂł����Ɛ^�������ɂȂ��Ă��܂��̂ł��B
�Ȃ�Ȃ����ϓ_���10�_�ȏ㍂���_������Ă��A���ʂ͏�ʂł͂Ȃ��̂ł��B
���v�_�̓���ɂ���Đ��т��ς��
���ʂ��オ�����A���������ň���J���Ă������P�B���鎞�����C���t���܂��B
�u���������ʂ��Ⴂ�q���A�������S�R���т��ǂ����ǁA�ǂ��������ƁH�v
�悭�C���t�����A����B
�����A���ʂ͂T���ȍ��v�_�ŏo��̂ɑ��āA���т͋��ȕʂɏo���̂ł��B
�Ⴆ���v300�_�̏ꍇ���l���Ă݂܂��B
�@�@�T���ȑS��60�_�̎q
�A�@1����80�_�A4����55�_
�B�@�Q����90�_�A�R����40�_
��L�R�Ƃ����v300�_�Ȃ̂ŁA�w�N���ʂ͓����ɂȂ�܂��B
�����A���ꂪ���тɂȂ��
�@�@�I�[��3
�A�@4���P�A3���S��
�B�@�T���Q�A�R��3��
�ɂȂ�\���������B
�������ʂȂ̂ɁA�B�̐l���_���g�c�Ő��т��ǂ��̂ł��B
����́A���т́u�R�v�����̂������L���_���܂ł��J�o�[�����Ƃ������Ƃ������ł��B
���т́u3�v�͂��Ȃ�L���͈͂܂ŃJ�o�[����
�������w���ɂȂ�A���т��T�i�K�ɂȂ��Ă킩�������Ƃ́A�u3�v�͂��̂������L���_���܂ŃJ�o�[�����A�Ƃ������ƁB
���ϓ_��葽�������Ă��u3�v����͐l�����z�}���猩�Ă��A�܂��Ó��B�������A���ϓ_���猋�\�Ⴍ�Ă��A��ۓI�ɂ͕��ϓ_��60�_�̏ꍇ�A20�_�キ�炢�܂Łu3�v�Ȃ̂ł��B
�u3�v�̒��ɂ��A3.0�`3.9�܂ŕ��z������A3.0�̐l��3.9�̐l�͒���e�X�g�Ŕ{�ȏ�_���Ⴄ�̂ɁA�������тɂȂ��Ă��܂��̂ł��B
�Ȃ̂ŕ��ϓ_�������������_�����̂����ѓI�ɂ͂P�Ԃ��������Ȃ��B
�������́A��o���A���Ƒԓx�Ȃǂ͖��Ȃ��̏ꍇ�ł��B
�w�N���ʂ͓��\�ɂ͊W������
���Ƌ��c�������ʁA���P�ł̊w�N���ʂƐ��сA���̓��ӁE�s���ӂ��l���A���Q�������e�X�g���𐬐т��グ������֕ύX�������܂����B
���ȋ��Ȃ́u3�v������Ηǂ��Ƃ��A�����Ԃ����������ɂ���B
���̑��蓾�ӂȋ��Ȃɕ����Ԃ����āA�ł��邾���ǂ��_������Đ��т��グ��A�Ƃ������ł��B
�������ʂ��������Ă��C�ɂ��Ȃ��B���\�͐��тȂ̂ŁA���ʂɂ������K�v�͂Ȃ��̂ł��B
�Ƃ͌����A���܂���s���Ӌ��Ȃ�����Ă����킯�ɂ͂����Ȃ����R�������܂��B
����́A�����͂T���ȍ��v�_�ŃW���b�W��������ƁB
�Ƃ͂����A�����͂T���ȍ��v�i�R���ȍ��v�j�ŃW���b�W�����
���т��グ������փV�t�g���A�e�X�g���ł͕s���Ӌ��Ȃɗ͂���ꂷ���Ȃ��A�Ƃ������ł��悤�ɂ��Ă���̂ł����A�Ƃ͌����s���Ӌ��Ȃ����Ă����Ȃ��Ȃ�͍���B
�����ł͕s���Ӌ��Ȃ��K�v������B
���̉��~���ƂĂ�����I
���̏ꍇ�A�s���Ӌ��Ȃ͂���Ă��ł��Ȃ������ɁA���Ȃ��ƑS���o���Ȃ��Ȃ��̂ł��B
�������s���Ӌ��Ȃ��P���Ȓ��x�Ȃ�Ηǂ����A���̏ꍇ�R���ȁi���E���E�Ёj������B�����ȏオ�s���ӂȂ�A���͂�����̂��̂��s���ӂȂ̂ł��A�Ƃ����C���炵�Ă���̂ł��B
�撣���āA���̎Љ�̐��т��グ�悤�Ƃ��Ă���b�͂�����B
�����������A���ȗ��j�̓_���オ�������@
�����������A���ȗ��j�̓_���オ�������@
���Ȑ��w�B�n���̂悤�Șb�͂�����B
�ȒP�Ȍv�Z�������܂ł����Ă��Ђ��Z�ł����
�ȒP�Ȍv�Z�������܂ł����Ă��Ђ��Z�ł����
���ȗ��ȁA�Љ�B�n���̂悤�Șb�͂�����B
���P�ŏ��̖͎��̗��ȂƎЉ�̕��l��30�䂾�����b
���P�ŏ��̖͎��̗��ȂƎЉ�̕��l��30�䂾�����b