さて、Laboratory初回になります。
…が、いきなりテーマ№6「自機に向かって飛んでくる敵弾」の考え方について説明します。
「自機に向かって飛んでくる敵弾」とは、シューティングゲーム等で、敵が撃った弾が自機に向かってゆっくり飛んできますよね。
あれをマシン語でどうやるか?を考えてみたいと思います。
実はこのテーマの実現のためには、
№2「マシン語の掛け算」
№3「マシン語の割り算」
№4「マシン語の平方根の求め方」
が必要になります。
なぜかと言うと、「三平方の定理」が必要となるからです。
■三平方の定理
斜辺(c)の2乗は、直角をはさむ辺(a、b)を2乗して足したものと等しい。
a² + b² = c²が成り立つ
斜辺(c)の2乗は、直角をはさむ辺(a、b)を2乗して足したものと等しい。
a² + b² = c²が成り立つ
これを利用します。
よって、今回は考え方のみで、実践はLaboratoryテーマ№2~4をした後続きをやることにします。
では、早速考え方です。
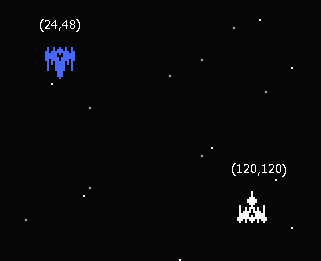
自機と敵がこの位置関係でいたとします。
この時、自機と敵のY軸とX軸との差と、自機と敵の座標を直接結ぶと、直角三角形が出来ます。
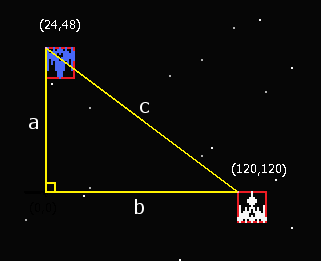
Y軸の長さをa、X軸の長さをb、自機と敵をつないだ線(斜辺)の長さをcとします。
これを三平方の定理で計算すると。
a =(120 - 48)= 72
b =(120 - 24)= 96
72² + 96² = 5,184 + 9,216 = 14,400 = c²
c = 120となります。
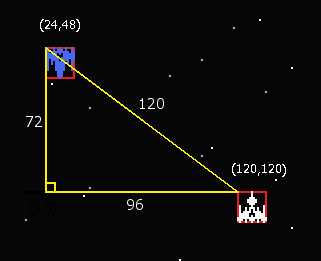
敵の弾がY軸が等しい自機に当たるまで96移動なので、距離120の自機に当たるまで120移動の必要があります。
よって、1移動当りの弾移動量を計算します。
Y方向 = 72(a)÷ 120(c)= 0.6
X方向 = 96(b)÷ 120(c)= 0.8
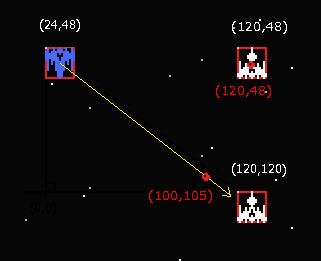
算出した移動量で96移動した時の弾の位置はこうなります。
Y座標:96 × 0.6 = 57.6 + 48(初期位置) = 105
X座標:96 × 0.8 = 76.8 + 24(初期位置) = 100
大体お解り頂けたでしょうか。
途中の計算で、掛け算(2乗算出、例:a²=a×a)、割り算、平方根(c²→c)が出てきましたね?
次回は、BASICで組んだ場合のサンプルを用意します。


