分かりやすい高校数学:確率(6)階乗!
前回 ⇒ 確率(5)確率の合成
確率の六回目ですー.更新遅れ気味なのを取り戻すべく,さくさくいってみよー.
前回,数え上げを計算するのに重要なことは二点あると言いました.今回はその一つ目,階乗についてです!
階乗とはなにか!それは,このびっくりマークを使って表現されます!たとえばー
3! = 3×2×1
5! = 5×4×3×2×1
8! = 8×7×6×5×4×3×2×1
と言うように,nという自然数があったとき,n!は1からnまでの数を掛け合わせた数値になります!
以上!!!(ぉい
これで終わったら解説にならんですね.さてさて,これは何に使うのでしょうか?
実は,並べ方の総数を計算するのに役に立つんです.
たとえば,「1から5までの数字が書かれた5個のボールがある時,そのボールの並べ方の総数は何通りか?」というような問題が出たら,5!です.って簡単に答えられます.すげー.
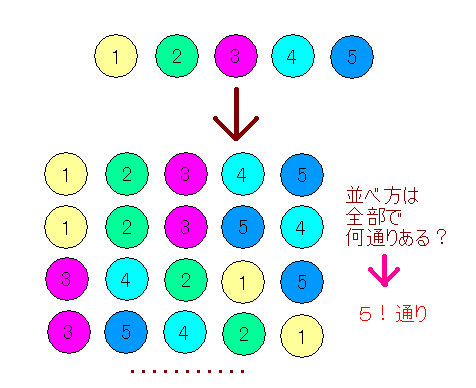
さて,ではなぜ,1から5までの数字が書かれたボールの並べ方の総数が5! になるのかについて考えてみましょう.
今,ボールは5個あるわけですが,その中の一つを選んで,先頭においてみます.この時,先頭のボールの選び方は5通りですね.次に,二つ目のボールを選ぶ方法は何通りあるでしょうか?これは図のようになります.
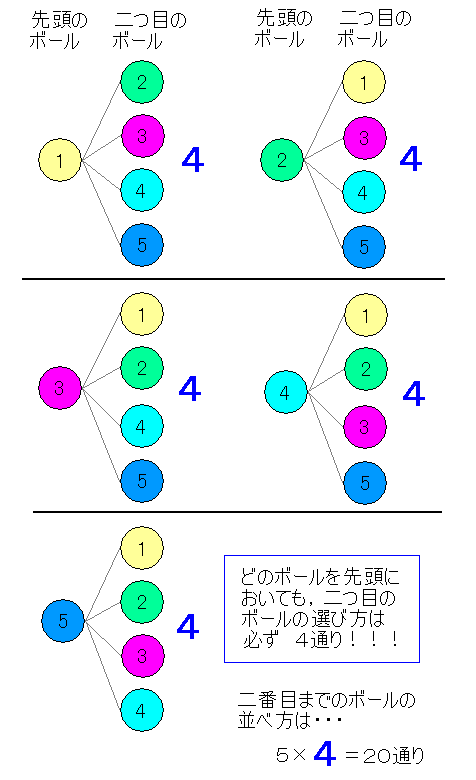
この時注目してほしいのは,先頭として選んだボールが何であっても,二番目のボールの選び方は必ず4通りになっているということです.二番目のボールを選ぶ際に,先頭に選んだボール以外から一つ選ぶということは,どんな場合でも変わらないからなんですね.
これを計算式で表すと,二番目のボールの選び方は,
5 (ボール全部) - 1 (先頭のボール) = 4通り (先頭のボール以外のボールの数)
と表現できます.よって,先頭と二番目のボール,二個分までの並べ方は,
5 (先頭のボールの選び方) × 4 (二つ目のボールの選び方) = 20通り
となります.このことは,先ほどの図からも分かりますね.
この考え方は,三つ目のボールを選ぶ時も変わりません.先頭と二番目のボールの選び方にかかわらず,常に残った3個のボールの中から選ぶことになります.よって,先頭,二番目,三番目までのボールの並べ方は,
5 (先頭のボールの選び方) × 4 (二番目のボールの選び方) × 3 (三番目のボールの選び方) = 60通り
となります.
これを最後まで,つまり五番目まで続けると・・・・
5 × 4 × 3 × 2 (四番目のボールの選び方) × 1 (五番目のボールの選び方)
となります.そう,これは5! と同じですね.
もし,問題文が「1から1000までの数字が書かれたボールの並べ方」について聞いている場合,1000×999×998×・・・・×2×1という計算式を書かなくてはいけなくなりますが,階乗という表現を使えば,1000! で表せます.これが階乗という考え方が導入されている理由です.
さて,ここで思い出してほしいのですが,先頭と二番目のボール,二個分までの並べ方は,5 (先頭のボールの選び方) × 4 (二つ目のボールの選び方) = 20通りあると言いました.ここで,5×4というこの式は,
5 × 4 = 5×4×3×2×1 (5!) ÷ 3×2×1 (3!)
とも書くことができます.これは,
5!(ボール全体の並べ方) ÷ 3!(先頭と二番目の二個分のボールの並べ方を考えるときに,使わなくて余ってしまったボールの並べ方)
って考えたりできませんか?!?

・・・・・・・・・・・・・・え?・・・できないですか,無理やりすぎですか.そうですね(笑)
かなり強引な展開をしましたが,なんと実はこの考え方は正しいのです.たとえば,先頭,二番目,三番目までのボールの並べ方は5×4×3でした.このとき,5個のボールのうち3個使ったのですから,余っているボールは2個です.先ほどの式を使うと,
5! (ボール全部) ÷ 2! (並べ方に使わなかった,余ったボール)
となります.そう,これは5×4×3と同じです!!!!
急な展開についてこれてない人もいるでしょう.突然でてきたこの計算方法がなぜ正しい解になるのか.それこそが,最初に言った,重要な二点のうちの二つ目なんですね.
それはまた次回!
全十回って前に言ったけど,もっと伸ばしたほうがよさそうな気がしてきました・・・予定は未定ってこのことなんだね...
次回 ⇒ 確率(7)順列
確率の六回目ですー.更新遅れ気味なのを取り戻すべく,さくさくいってみよー.
前回,数え上げを計算するのに重要なことは二点あると言いました.今回はその一つ目,階乗についてです!
階乗とはなにか!それは,このびっくりマークを使って表現されます!たとえばー
3! = 3×2×1
5! = 5×4×3×2×1
8! = 8×7×6×5×4×3×2×1
と言うように,nという自然数があったとき,n!は1からnまでの数を掛け合わせた数値になります!
以上!!!(ぉい
これで終わったら解説にならんですね.さてさて,これは何に使うのでしょうか?
実は,並べ方の総数を計算するのに役に立つんです.
たとえば,「1から5までの数字が書かれた5個のボールがある時,そのボールの並べ方の総数は何通りか?」というような問題が出たら,5!です.って簡単に答えられます.すげー.
| ◆ 付け足しメモ ◆ ・・・まー高校の授業なんかでは,5! = 5×4×3×2×1もきちんと計算して,「120です」って答えないといけないですけどね.そんな夢のない話はおいておいて(笑). |
さて,ではなぜ,1から5までの数字が書かれたボールの並べ方の総数が5! になるのかについて考えてみましょう.
今,ボールは5個あるわけですが,その中の一つを選んで,先頭においてみます.この時,先頭のボールの選び方は5通りですね.次に,二つ目のボールを選ぶ方法は何通りあるでしょうか?これは図のようになります.
この時注目してほしいのは,先頭として選んだボールが何であっても,二番目のボールの選び方は必ず4通りになっているということです.二番目のボールを選ぶ際に,先頭に選んだボール以外から一つ選ぶということは,どんな場合でも変わらないからなんですね.
これを計算式で表すと,二番目のボールの選び方は,
5 (ボール全部) - 1 (先頭のボール) = 4通り (先頭のボール以外のボールの数)
と表現できます.よって,先頭と二番目のボール,二個分までの並べ方は,
5 (先頭のボールの選び方) × 4 (二つ目のボールの選び方) = 20通り
となります.このことは,先ほどの図からも分かりますね.
この考え方は,三つ目のボールを選ぶ時も変わりません.先頭と二番目のボールの選び方にかかわらず,常に残った3個のボールの中から選ぶことになります.よって,先頭,二番目,三番目までのボールの並べ方は,
5 (先頭のボールの選び方) × 4 (二番目のボールの選び方) × 3 (三番目のボールの選び方) = 60通り
となります.
これを最後まで,つまり五番目まで続けると・・・・
5 × 4 × 3 × 2 (四番目のボールの選び方) × 1 (五番目のボールの選び方)
となります.そう,これは5! と同じですね.
もし,問題文が「1から1000までの数字が書かれたボールの並べ方」について聞いている場合,1000×999×998×・・・・×2×1という計算式を書かなくてはいけなくなりますが,階乗という表現を使えば,1000! で表せます.これが階乗という考え方が導入されている理由です.
さて,ここで思い出してほしいのですが,先頭と二番目のボール,二個分までの並べ方は,5 (先頭のボールの選び方) × 4 (二つ目のボールの選び方) = 20通りあると言いました.ここで,5×4というこの式は,
5 × 4 = 5×4×3×2×1 (5!) ÷ 3×2×1 (3!)
とも書くことができます.これは,
5!(ボール全体の並べ方) ÷ 3!(先頭と二番目の二個分のボールの並べ方を考えるときに,使わなくて余ってしまったボールの並べ方)
って考えたりできませんか?!?
・・・・・・・・・・・・・・え?・・・できないですか,無理やりすぎですか.そうですね(笑)
かなり強引な展開をしましたが,なんと実はこの考え方は正しいのです.たとえば,先頭,二番目,三番目までのボールの並べ方は5×4×3でした.このとき,5個のボールのうち3個使ったのですから,余っているボールは2個です.先ほどの式を使うと,
5! (ボール全部) ÷ 2! (並べ方に使わなかった,余ったボール)
となります.そう,これは5×4×3と同じです!!!!
急な展開についてこれてない人もいるでしょう.突然でてきたこの計算方法がなぜ正しい解になるのか.それこそが,最初に言った,重要な二点のうちの二つ目なんですね.
それはまた次回!
全十回って前に言ったけど,もっと伸ばしたほうがよさそうな気がしてきました・・・予定は未定ってこのことなんだね...
確率は,最終的には統計学などを使いこなせるようになるための基礎とも言えるわけですが,統計や検定部分は,高校数学ではあまり扱われていません.つまり,本来の使い方まで至らずに終わってしまっているわけですね.そこまでの道のりを知っているかどうか,つまり何の役にたつものなのかを知ることは,モチベーションにも関わってきます.
この本ではコンパクトな冊子ながら,初心者に分かりやすく,確率・統計を教えてくれる良本です.読みながすだけでも価値ありだと思います. |
次回 ⇒ 確率(7)順列
【確率の最新記事】








この記事へのコメント