分かりやすい高校数学:確率(12)実際の問題に対して(後編)
前回 ⇒ 確率(11):実際の問題に対して(前編)
前回に引き続いて，確率の問題に対する心構えのようなお話をしていきたいと思います．前回をご覧になってない方は上のリンクからどうぞ〜．
さて，いかに問題を切り分けて楽に計算するか，ということをお気づきいただけたでしょうか？ここで一つ，簡単に計算できるテクニックについてお話しましょう．ずばり余事象の考え方です！
余事象というのは，注目したある事象以外の事象のことを指します（余っちゃった事象ということですね）．たとえば，「１が出る」事象の余事象は「１がでない」事象となります．
「１が出ない」事象は具体的にいえば「２，３，４，５，６のいずれかが出る」事象となるのですが，ご覧の通り事象の数が多いです．しかし，これを簡単に計算する方法があるのです．それは，「全体から元の事象を引く」というものです．ちょっと実例を見てみましょう．
「１〜９までの数字が書かれた９個のボールから５個選んで並べる際に，偶数が書かれたボールが２つ入っていない並べ方は何通りか？」
これは先ほど，最初の問題と似ていますが，最後に否定が付いています．つまり，最初の問題で求めようとした事象の余事象についての問題です．考えただけでも大変そうなこの問題が，余事象を使えばとても簡単に解けます．
まずは全体を求めましょう．つまり９個のボールから５個選んで並べる方法です．これは簡単ですね．そう9P5=15120通りですね．
そして，「１〜９までの数字が書かれた９個のボールから５個選んで並べる際に，偶数が書かれたボールが２つ入っていている並べ方」は先ほど求めたように，7200通りです．よって，この問題の答えは，15120 - 7200 = 7920通りとなります．
とても簡単ですね．この余事象の考え方は順列はもちろん，確率でも使えます．確率の場合は１から引けば良いのです．余事象を上手く使いこなせると楽ができますよ！特に，「〜じゃない場合」とか，「〜以外である場合」とかの言葉が出てきたら余事象を疑うとよいですね．
さて，最後に，この分野の大目標である，確率へとつなげましょう．これが最後の問題です．
「１〜９までの数字が書かれた９個のボールから５個選んで並べる際に，偶数が書かれたボールが２つ入ってる確率はいくらか？」
これは最初の問題の解，7200を並べ方の総数である15120で割ればよいですよね．よって，7200 / 15120 = 10 / 21です．あら，あっさり(笑)．
確率は順列や組み合わせを全体の順列・組み合わせで割ることで得られます．よって，確率は順列や組み合わせと計算方法が似通っています．ただし，確率で注意しなければいけないのは，数え上げによる確率計算の規則を満たしているかどうかです．特に，「同様に確からしい」かどうかは注意が必要です．これは騙されやすいので注意してください．
よく騙される例を一つ挙げてみます．ある人が図のＡ地点からＢ地点へ向かうとします．このとき，その人は上か右にしか行けません．また，上にも右にもいけるときには，ランダムにどちらか一方に進むとします．そのとき，経路はa, b, c の三通り存在します．さて，それでは経路aを通って行く確率はいくらでしょうか？
数え上げで考えようとすると，経路は３本あるから，1/3だろうと考えたくなります．しかしこの解答は間違いです．この３本の経路は「同様に確からしい」と言えないからです．なぜでしょうか？
重要なのは，道の選択をする必要がある分岐点の数となります．それぞれの経路の「上・右」への分岐点を数えてみると，下のようになります．
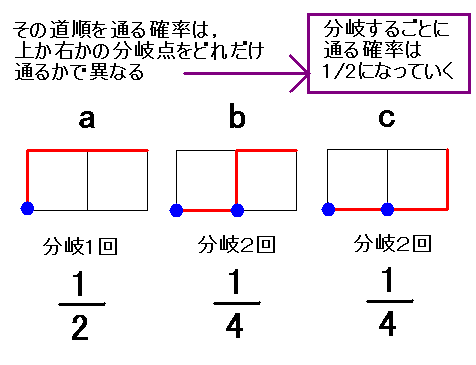
これをみると，経路aは分岐点が1個なのに対し，経路b,c は２個あります．そう，「同様に確からしい」という条件が満たされていないわけですね．実際の経路aの確率は，分岐一回分なので1/2となります．ちなみに経路b,c は分岐二回なので，1/2×1/2=1/4となります．順列・組み合わせでは，「同様に確からしい」かを考える必要はありませんが，そこから確率を計算する場合には十分に注意してくださいね．
さて，以上で本編は終了です．以降は補足や読み物系の話をしようかと考えています．実際には円順列や数珠順列，重複あり順列など，細かい話があったり，確率の加法定理とか難しそうな用語とかあったりするのですが，そこは話をややこしくするだけなので，本編では触れませんでした．ポイントだけすっきりおさえるに専念したかったからです．なので，これ以降で少しずつ補足しようかと思っています．まぁ，あんまり補足すると他と変わらないので，そんなにやる気はないのですが（笑）
次からの回は簡単に，読み物系にしようと思っています．予定として，「サイコロを沢山ふっているけど，最近１が出ていない！次は１がでやすいはず！」という考え方は正しいか？！という話についてです．正解をいっちゃうと間違いなんですが，なぜ間違いなのかについてわかりやすく説明してみたいと思います．
それでは〜
次 ⇒ 確率(番外1):大数の法則
前回に引き続いて，確率の問題に対する心構えのようなお話をしていきたいと思います．前回をご覧になってない方は上のリンクからどうぞ〜．
さて，いかに問題を切り分けて楽に計算するか，ということをお気づきいただけたでしょうか？ここで一つ，簡単に計算できるテクニックについてお話しましょう．ずばり余事象の考え方です！
余事象というのは，注目したある事象以外の事象のことを指します（余っちゃった事象ということですね）．たとえば，「１が出る」事象の余事象は「１がでない」事象となります．
「１が出ない」事象は具体的にいえば「２，３，４，５，６のいずれかが出る」事象となるのですが，ご覧の通り事象の数が多いです．しかし，これを簡単に計算する方法があるのです．それは，「全体から元の事象を引く」というものです．ちょっと実例を見てみましょう．
「１〜９までの数字が書かれた９個のボールから５個選んで並べる際に，偶数が書かれたボールが２つ入っていない並べ方は何通りか？」
これは先ほど，最初の問題と似ていますが，最後に否定が付いています．つまり，最初の問題で求めようとした事象の余事象についての問題です．考えただけでも大変そうなこの問題が，余事象を使えばとても簡単に解けます．
まずは全体を求めましょう．つまり９個のボールから５個選んで並べる方法です．これは簡単ですね．そう9P5=15120通りですね．
そして，「１〜９までの数字が書かれた９個のボールから５個選んで並べる際に，偶数が書かれたボールが２つ入っていている並べ方」は先ほど求めたように，7200通りです．よって，この問題の答えは，15120 - 7200 = 7920通りとなります．
とても簡単ですね．この余事象の考え方は順列はもちろん，確率でも使えます．確率の場合は１から引けば良いのです．余事象を上手く使いこなせると楽ができますよ！特に，「〜じゃない場合」とか，「〜以外である場合」とかの言葉が出てきたら余事象を疑うとよいですね．
さて，最後に，この分野の大目標である，確率へとつなげましょう．これが最後の問題です．
「１〜９までの数字が書かれた９個のボールから５個選んで並べる際に，偶数が書かれたボールが２つ入ってる確率はいくらか？」
これは最初の問題の解，7200を並べ方の総数である15120で割ればよいですよね．よって，7200 / 15120 = 10 / 21です．あら，あっさり(笑)．
確率は順列や組み合わせを全体の順列・組み合わせで割ることで得られます．よって，確率は順列や組み合わせと計算方法が似通っています．ただし，確率で注意しなければいけないのは，数え上げによる確率計算の規則を満たしているかどうかです．特に，「同様に確からしい」かどうかは注意が必要です．これは騙されやすいので注意してください．
よく騙される例を一つ挙げてみます．ある人が図のＡ地点からＢ地点へ向かうとします．このとき，その人は上か右にしか行けません．また，上にも右にもいけるときには，ランダムにどちらか一方に進むとします．そのとき，経路はa, b, c の三通り存在します．さて，それでは経路aを通って行く確率はいくらでしょうか？
数え上げで考えようとすると，経路は３本あるから，1/3だろうと考えたくなります．しかしこの解答は間違いです．この３本の経路は「同様に確からしい」と言えないからです．なぜでしょうか？
重要なのは，道の選択をする必要がある分岐点の数となります．それぞれの経路の「上・右」への分岐点を数えてみると，下のようになります．
これをみると，経路aは分岐点が1個なのに対し，経路b,c は２個あります．そう，「同様に確からしい」という条件が満たされていないわけですね．実際の経路aの確率は，分岐一回分なので1/2となります．ちなみに経路b,c は分岐二回なので，1/2×1/2=1/4となります．順列・組み合わせでは，「同様に確からしい」かを考える必要はありませんが，そこから確率を計算する場合には十分に注意してくださいね．
さて，以上で本編は終了です．以降は補足や読み物系の話をしようかと考えています．実際には円順列や数珠順列，重複あり順列など，細かい話があったり，確率の加法定理とか難しそうな用語とかあったりするのですが，そこは話をややこしくするだけなので，本編では触れませんでした．ポイントだけすっきりおさえるに専念したかったからです．なので，これ以降で少しずつ補足しようかと思っています．まぁ，あんまり補足すると他と変わらないので，そんなにやる気はないのですが（笑）
次からの回は簡単に，読み物系にしようと思っています．予定として，「サイコロを沢山ふっているけど，最近１が出ていない！次は１がでやすいはず！」という考え方は正しいか？！という話についてです．正解をいっちゃうと間違いなんですが，なぜ間違いなのかについてわかりやすく説明してみたいと思います．
それでは〜
数学の問題を解くってのは，いつの時代も大変だったんだなーと思わせてくれる本がコレ！
うぉ！なんてレトロな表紙（笑）いかにもって感じで古い表紙なのに，いまだに現役な本です．なんでもWindowsなどを作成しているマイクロソフト社員は必読の書なんだとか！？原著が刊行されたのは1956年だというのだから凄い．もう50年以上たってますぜ（笑） でも，中身は今でも通じるほどに価値あり．問題を解くためにはどうしたらいいのかという，基本的なところを分かりやすく説明しています．もうバイブルみたいな感じっすね． |
次 ⇒ 確率(番外1):大数の法則
【確率の最新記事】
確率１
この記事へのコメント