•ھ‚©‚è‚â‚·‚¢چ‚چZگ”ٹw:ٹm—¦(4)گ”‚¦ڈم‚°‚جڈًŒڈ
‘O‰ٌپ@پثپ@ٹm—¦(3)گ”‚¦ڈم‚°
‚³‚ؤپCچ،‰ٌ‚حگ”‚¦ڈم‚°‚ة‚و‚éٹm—¦ŒvژZ‚ً‚µ‚ؤ‚و‚¢‚©‚ً”»’f‚·‚éڈم‚إ‚جپCڈًŒڈ‚ة‚آ‚¢‚ؤ‚إ‚·پD
ڈًŒڈ‚ًچl‚¦‚éڈم‚إڈd—v‚ب‚ج‚حپCگ”‚¦ڈم‚°‚ة‚و‚éٹm—¦‚جŒvژZژ®پ@–ع“I‚جژ–ڈغ‚جگ”پ@÷پ@”گ¶‚µ‚¤‚éژ–ڈغ‚جگ”پ@‚ة‚¨‚¢‚ؤپCپu”گ¶‚µ‚¤‚éژ–ڈغ‚جگ”پv‚حژژچs‘S‘ج‚ج‘ه‚«‚³‚ً•\Œ»‚µ‚ؤ‚¢‚é‚ئ‚¢‚¤‚±‚ئ‚إ‚·پDژژچs‘S‘ج‚ة‘خ‚·‚é–ع“I‚جژ–ڈغ‚جٹ„چ‡‚ًŒvژZ‚·‚é‚ج‚ھپCٹm—¦‚¾‚©‚ç‚إ‚·‚ثپD‚و‚ء‚ؤپC‚±‚ج•”•ھ‚ھگ³ٹm‚ةپuژژچs‘S‘ج‚ج‘ه‚«‚³پv‚ً•\Œ»‚إ‚«‚ؤ‚¢‚ب‚¢‚ئپCگ”‚¦‚ ‚°‚إ‚جٹm—¦ŒvژZ‚ح‚إ‚«‚ـ‚¹‚ٌپD
‚³‚ؤپC‚إ‚ح‚ا‚ٌ‚بڈًŒڈ‚ھ‚ ‚肤‚é‚ج‚©پIƒYƒoƒٹŒ¾‚ء‚ؤ‚µ‚ـ‚¤‚ئپC‚»‚جڈًŒڈ‚حژO‚آ‚ ‚è‚ـ‚·پI
‡@ٹeژ–ڈغ‚ھپu“¯—l‚ةٹm‚©‚炵‚¢پv‚±‚ئپ@پپپ@‚ا‚جژ–ڈغ‚ج”گ¶‚·‚éٹm—¦‚à“™‚µ‚¢‚±‚ئ
‚±‚ê‚ح‘O‰ٌگG‚ꂽ•”•ھ‚إ‚·‚ثپD‚آ‚ـ‚èپC‚»‚ꂼ‚ê‚جژ–ڈغ‚جڈoŒ»گ”‚ً‘S•”‚P‚ئ‚ف‚ب‚µ‚ؤپCژژچs‘S‘جپi”گ¶‚µ‚¤‚éژ–ڈغ‚جگ”پj‚ًŒvژZ‚µ‚ؤ‚¢‚é‚ج‚إپC‚·‚ׂؤ‚جژ–ڈغ‚جٹm—¦‚ھ“™‚µ‚‚ب‚¢‚ئ‚¢‚¯‚ـ‚¹‚ٌپD‚PپD‚T”{‚ئ‚©‚R”{‚ئ‚©‚ج”گ¶ٹm—¦‚ًژ‚آژ–ڈغ‚ھچ¬‚´‚ء‚ؤ‚¢‚½‚肵‚ؤ‚ح‚¢‚¯‚ب‚¢‚ي‚¯‚إ‚·پD
‚إ‚·‚ج‚إپCپu‚P‚©‚Q‚ھڈo‚éژ–ڈغپv‚ئپu‚R‚©‚S‚©‚T‚©‚U‚ھڈo‚éژ–ڈغپv‚ج“ٌ‚آ‚جژ–ڈغ‚ًچl‚¦‚½‚ئ‚«پCپu‚P‚©‚Q‚ھڈo‚éژ–ڈغپv‚جٹm—¦‚ح1/2‚¾پI‚ئ‚ح‚إ‚«‚ـ‚¹‚ٌپD‚±‚ج“ٌ‚آ‚جژ–ڈغ‚جٹm—¦‚ح–¾‚ç‚©‚ة“™‚µ‚‚ب‚¢‚©‚ç‚إ‚·پD
‚±‚ê‚ھپCپu‚P‚©‚Q‚©‚R‚ھڈo‚éژ–ڈغپv‚ئپu‚S‚©‚T‚©‚U‚ھڈo‚éژ–ڈغپv‚ج“ٌ‚آ‚جژ–ڈغ‚ًچl‚¦‚ؤپCپu‚P‚©‚Q‚©‚R‚ھڈo‚éژ–ڈغپv‚جٹm—¦‚ح1/2‚¾پI‚ئ‚¢‚¤‚±‚ئ‚ح‚إ‚«‚ـ‚·پD‚±‚ê‚حپC“ٌ‚آ‚جژ–ڈغ‚جٹm—¦‚ھپu“¯—l‚ةٹm‚©‚炵‚¢پv‚ئ”»’f‚إ‚«‚é‚©‚ç‚إ‚·پD

پu‚P‚©‚Q‚©‚R‚ھڈo‚éژ–ڈغپv‚ئپu‚S‚©‚T‚©‚U‚ھڈo‚éژ–ڈغپv‚حپu“¯—l‚ةٹm‚©‚炵‚¢پv‚±‚ئ‚حپC‚»‚ꂼ‚ê‚ج–ع‚ھڈo‚邱‚ئ‚ھپu“¯—l‚ةٹm‚©‚炵‚¢پv‚±‚ئ‚©‚ç•ھ‚©‚è‚ـ‚·پD‚ا‚؟‚ç‚جژ–ڈغ‚àپC‚ ‚é–ع‚ھڈo‚éژ–ڈغ‚ًژO‚آ•ھ‘«‚µ‚½ژ–ڈغ‚ئ‚ب‚ء‚ؤ‚¢‚é‚©‚ç‚إ‚·پD‚µ‚©‚µپCڈي‚ةپu“¯—l‚ةٹm‚©‚炵‚¢پv‚±‚ئ‚ھ•ھ‚©‚é‚ئ‚حŒہ‚è‚ـ‚¹‚ٌپD‚½‚ئ‚¦‚خ‘O‰ٌ‚جکb‚ة‚ ‚ء‚½‚و‚¤‚ب’¼•û‘ج‚جƒTƒCƒRƒچ‚جڈêچ‡پC–ع‚جڈo•û‚ھپu“¯—l‚ةٹm‚©‚炵‚¢پv‚©‚ح‚ي‚©‚è‚ـ‚¹‚ٌپD‚ذ‚ه‚ء‚ئ‚µ‚½‚çپu“¯—l‚ةٹm‚©‚炵‚¢پv‚©‚à‚µ‚ê‚ب‚¢‚ج‚إ‚·‚ھپC‚»‚¤‚إ‚ ‚é‚ئ”»’f‚إ‚«‚ب‚¢‚ب‚çژg‚ء‚ؤ‚ح‚¢‚¯‚ـ‚¹‚ٌپD
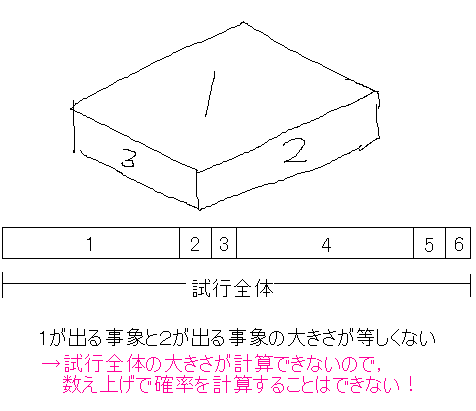
‡A‘S‚ؤ‚جژ–ڈغ‚ًچ‡‚ي‚¹‚é‚ئپCژژچs‘S‘ج‚جژ–ڈغ‚ً‘S•”•\‚¹‚é
‘Oڈq‚ج‚و‚¤‚ةپC‘S•”‚جژ–ڈغ‚ًچ‡‚ي‚¹‚½‚ئ‚«‚ةپCژژچs‘S‘ج‚ً•\Œ»‚إ‚«‚ؤ‚¢‚ب‚¢‚ئ‚¢‚¯‚ـ‚¹‚ٌپD‚و‚ء‚ؤپCپu‚P‚ھڈo‚éژ–ڈغپv‚ئپu‚Q‚ھڈo‚éژ–ڈغپv‚ج“ٌ‚آ‚جژ–ڈغ‚ًچl‚¦‚ؤپCپu‚P‚ھڈo‚éژ–ڈغپv‚ح1/2‚¾پI‚ئ‚حŒ¾‚¦‚ب‚¢‚ي‚¯‚إ‚·پDپu‚P‚ھڈo‚éژ–ڈغپv‚ئپu‚Q‚ھڈo‚éژ–ڈغپv‚¾‚¯‚إ‚حپCژژچs‘S‘ج‚ً•\Œ»‚إ‚«‚ؤ‚¢‚ب‚¢‚©‚ç‚إ‚·‚ثپD
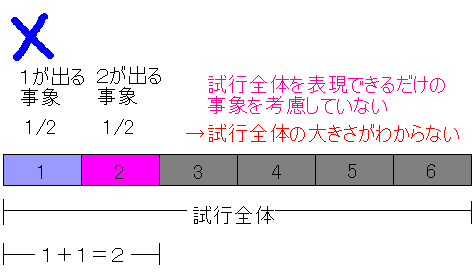
‡B‚»‚ꂼ‚ê‚جژ–ڈغ‚جٹش‚إڈd‚ب‚ء‚ؤ‚¢‚é•”•ھ‚ھ‚ب‚¢
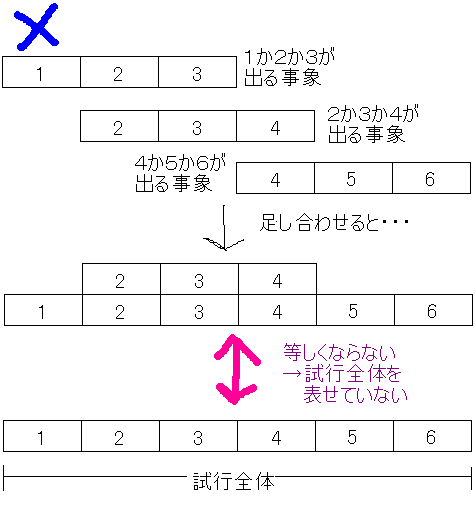
‚à‚µژژچs‘S‘ج‚ج‘ه‚«‚³‚ًŒvژZ‚·‚é‚ئ‚«‚ةپCٹـ‚ـ‚ê‚éژ–ڈغ‚ً“ٌڈd‚ةŒvژZ‚µ‚ؤ‚µ‚ـ‚¤‚ئپCژژچs‘S‘ج‚جگ³ٹm‚ب‘ه‚«‚³‚إ‚ح‚ب‚‚ب‚è‚ـ‚·پD‚½‚ئ‚¦‚خپCپu‚P‚©‚Q‚©‚R‚ھڈo‚éژ–ڈغپv‚ئپu‚Q‚©‚R‚©‚S‚ھڈo‚éژ–ڈغپv‚ئپu‚S‚©‚T‚©‚U‚ھڈo‚éژ–ڈغپv‚ئ‚¢‚¤ژO‚آ‚جژ–ڈغ‚ًچl‚¦‚ؤپCپu‚P‚©‚Q‚©‚R‚ھڈo‚éژ–ڈغپv‚جٹm—¦‚ح1/3‚إ‚·پI‚ئ‚حŒ¾‚¦‚ـ‚¹‚ٌپD
‚ب‚؛‚ب‚ç‚خپC‘S‘ج‚ً‘«‚µچ‡‚ي‚¹‚½‚ئ‚«‚ةپCپu‚Q‚ھڈo‚éژ–ڈغپvپu‚R‚ھڈo‚éژ–ڈغپvپu‚S‚ھڈo‚éژ–ڈغپv‚ً“ٌ‰ٌٹـ‚ٌ‚إ‚µ‚ـ‚ء‚ؤ‚¢‚é‚ج‚إپC‚±‚ê‚ç‚ً‘«‚µچ‡‚ي‚¹‚ؤ‚àپCژژچs‘S‘ج‚ج‘ه‚«‚³‚ًگ³ٹm‚ة“¾‚ç‚ê‚ب‚¢‚©‚ç‚ب‚ٌ‚إ‚·‚ثپD
‚³‚ؤپC‚±‚±‚إگV‚µ‚—pŒê‚ً“±“ü‚µ‚ـ‚·پC“ٌ‚آ‚جژ–ڈغ‚ھڈd‚ب‚ء‚ؤ‚¢‚ب‚¢پC‚ئ‚¢‚¤‚±‚ئ‚ًپC“ٌ‚آ‚جژ–ڈغ‚ھ”r‘¼“I‚إ‚ ‚éپC‚ئ‚¢‚¢‚ـ‚·پD‚±‚¤‚¢‚¤Œ¾—t‚ھ‚³‚ç‚ء‚ئژg‚¦‚é‚و‚¤‚ة‚ب‚é‚ئ‚ب‚ٌ‚©ƒJƒbƒR‚¢‚¢ٹ´‚¶‚ھ‚µ‚ـ‚¹‚ٌ‚©پI‚µ‚ب‚¢‚إ‚·‚و‚ثپI‚»‚¤‚إ‚·‚ثپI‚±‚¤‚¢‚¤Œ¾—t‚ً‚³‚ç‚ء‚ئژg‚¤‚ج‚حگ³’¼پC—Œn‚¾‚¯‚إ‚·پiڈخپj

‚±‚±‚ـ‚إ—ˆ‚ê‚خٹm—¦‚ح‚ظ‚ئ‚ٌ‚ا•ھ‚©‚ء‚½‚à“¯‘RپIپi‘½•ھ‚ثپIپjپD
‚ ‚ئڈd—v‚ب‚ج‚حپCٹm—¦‚جچ‡گ¬•”•ھ‚إ‚·پD“ٌ‚آ‚جƒTƒCƒRƒچ‚ًگU‚ء‚½ژ‚جٹm—¦‚ح‚ا‚¤‚ب‚é‚جپH‚ئ‚¢‚¤‚ئ‚±‚ë‚إ‚·‚ثپD‚؟‚ب‚ف‚ةپCˆê‚آ‚جƒTƒCƒRƒچ‚ًگU‚ء‚½ژ‚جٹm—¦‚ً‘«‚µچ‡‚ي‚¹‚éکb‚à‚ ‚è‚ـ‚·‚ھپCچ،‚ـ‚إ‚جگà–¾‚©‚ç‘ه‘ج‚»‚ج“ڑ‚¦‚حŒ©‚¦‚ؤ‚¢‚é‚©‚ئژv‚¢‚ـ‚·پD‚à‚؟‚ë‚ٌپC‚±‚ج“_‚àژں‰ٌپCˆêڈڈ‚ةگà–¾‚µ‚½‚¢‚ئژv‚¢‚ـ‚·پD
‚à‚¤ˆê“_ڈd—v‚ب‚ج‚حپCگ”‚¦ڈم‚°‚جŒّ—¦“I‚ب•û–@‚إ‚·‚ثپDƒTƒCƒRƒچ‚‚ç‚¢‚ب‚çٹب’P‚ةژ–ڈغ‚ًگ”‚¦‚ç‚ê‚ـ‚·‚ھپC‚à‚ء‚ئ•،ژG‚ة‚ب‚é‚ئ‘ه•د‚إ‚·پD‚»‚ج‚½‚ك‚جƒeƒNƒjƒbƒN‚ة‚آ‚¢‚ؤ‚à•×‹‚·‚é•K—v‚ھ‚ ‚è‚ـ‚·پD‹t‚ةŒ¾‚¦‚خپCچ‚چZگ”ٹwA‚إڈd—v‚ب‚ج‚حپC‚à‚¤‚»‚ج“ٌ‚آ‚‚ç‚¢‚µ‚©‚ب‚©‚ء‚½‚肵‚ـ‚·پiچ،‚جگV‰غ’ِ‚ئ‚©‚إ‚حگFپXˆل‚ء‚½‚è‚·‚é‚©‚à‚µ‚ê‚ب‚¢‚¯‚اپOپOپjپD
‚»‚ج•س‚ح‚à‚¤ڈ‚µگو‚إپI
‘±‚«پ@پثپ@ٹm—¦(5)ٹm—¦‚جچ‡گ¬
‚³‚ؤپCچ،‰ٌ‚حگ”‚¦ڈم‚°‚ة‚و‚éٹm—¦ŒvژZ‚ً‚µ‚ؤ‚و‚¢‚©‚ً”»’f‚·‚éڈم‚إ‚جپCڈًŒڈ‚ة‚آ‚¢‚ؤ‚إ‚·پD
ڈًŒڈ‚ًچl‚¦‚éڈم‚إڈd—v‚ب‚ج‚حپCگ”‚¦ڈم‚°‚ة‚و‚éٹm—¦‚جŒvژZژ®پ@–ع“I‚جژ–ڈغ‚جگ”پ@÷پ@”گ¶‚µ‚¤‚éژ–ڈغ‚جگ”پ@‚ة‚¨‚¢‚ؤپCپu”گ¶‚µ‚¤‚éژ–ڈغ‚جگ”پv‚حژژچs‘S‘ج‚ج‘ه‚«‚³‚ً•\Œ»‚µ‚ؤ‚¢‚é‚ئ‚¢‚¤‚±‚ئ‚إ‚·پDژژچs‘S‘ج‚ة‘خ‚·‚é–ع“I‚جژ–ڈغ‚جٹ„چ‡‚ًŒvژZ‚·‚é‚ج‚ھپCٹm—¦‚¾‚©‚ç‚إ‚·‚ثپD‚و‚ء‚ؤپC‚±‚ج•”•ھ‚ھگ³ٹm‚ةپuژژچs‘S‘ج‚ج‘ه‚«‚³پv‚ً•\Œ»‚إ‚«‚ؤ‚¢‚ب‚¢‚ئپCگ”‚¦‚ ‚°‚إ‚جٹm—¦ŒvژZ‚ح‚إ‚«‚ـ‚¹‚ٌپD
‚³‚ؤپC‚إ‚ح‚ا‚ٌ‚بڈًŒڈ‚ھ‚ ‚肤‚é‚ج‚©پIƒYƒoƒٹŒ¾‚ء‚ؤ‚µ‚ـ‚¤‚ئپC‚»‚جڈًŒڈ‚حژO‚آ‚ ‚è‚ـ‚·پI
‡@ٹeژ–ڈغ‚ھپu“¯—l‚ةٹm‚©‚炵‚¢پv‚±‚ئپ@پپپ@‚ا‚جژ–ڈغ‚ج”گ¶‚·‚éٹm—¦‚à“™‚µ‚¢‚±‚ئ
‚±‚ê‚ح‘O‰ٌگG‚ꂽ•”•ھ‚إ‚·‚ثپD‚آ‚ـ‚èپC‚»‚ꂼ‚ê‚جژ–ڈغ‚جڈoŒ»گ”‚ً‘S•”‚P‚ئ‚ف‚ب‚µ‚ؤپCژژچs‘S‘جپi”گ¶‚µ‚¤‚éژ–ڈغ‚جگ”پj‚ًŒvژZ‚µ‚ؤ‚¢‚é‚ج‚إپC‚·‚ׂؤ‚جژ–ڈغ‚جٹm—¦‚ھ“™‚µ‚‚ب‚¢‚ئ‚¢‚¯‚ـ‚¹‚ٌپD‚PپD‚T”{‚ئ‚©‚R”{‚ئ‚©‚ج”گ¶ٹm—¦‚ًژ‚آژ–ڈغ‚ھچ¬‚´‚ء‚ؤ‚¢‚½‚肵‚ؤ‚ح‚¢‚¯‚ب‚¢‚ي‚¯‚إ‚·پD
‚إ‚·‚ج‚إپCپu‚P‚©‚Q‚ھڈo‚éژ–ڈغپv‚ئپu‚R‚©‚S‚©‚T‚©‚U‚ھڈo‚éژ–ڈغپv‚ج“ٌ‚آ‚جژ–ڈغ‚ًچl‚¦‚½‚ئ‚«پCپu‚P‚©‚Q‚ھڈo‚éژ–ڈغپv‚جٹm—¦‚ح1/2‚¾پI‚ئ‚ح‚إ‚«‚ـ‚¹‚ٌپD‚±‚ج“ٌ‚آ‚جژ–ڈغ‚جٹm—¦‚ح–¾‚ç‚©‚ة“™‚µ‚‚ب‚¢‚©‚ç‚إ‚·پD
‚±‚ê‚ھپCپu‚P‚©‚Q‚©‚R‚ھڈo‚éژ–ڈغپv‚ئپu‚S‚©‚T‚©‚U‚ھڈo‚éژ–ڈغپv‚ج“ٌ‚آ‚جژ–ڈغ‚ًچl‚¦‚ؤپCپu‚P‚©‚Q‚©‚R‚ھڈo‚éژ–ڈغپv‚جٹm—¦‚ح1/2‚¾پI‚ئ‚¢‚¤‚±‚ئ‚ح‚إ‚«‚ـ‚·پD‚±‚ê‚حپC“ٌ‚آ‚جژ–ڈغ‚جٹm—¦‚ھپu“¯—l‚ةٹm‚©‚炵‚¢پv‚ئ”»’f‚إ‚«‚é‚©‚ç‚إ‚·پD
پu‚P‚©‚Q‚©‚R‚ھڈo‚éژ–ڈغپv‚ئپu‚S‚©‚T‚©‚U‚ھڈo‚éژ–ڈغپv‚حپu“¯—l‚ةٹm‚©‚炵‚¢پv‚±‚ئ‚حپC‚»‚ꂼ‚ê‚ج–ع‚ھڈo‚邱‚ئ‚ھپu“¯—l‚ةٹm‚©‚炵‚¢پv‚±‚ئ‚©‚ç•ھ‚©‚è‚ـ‚·پD‚ا‚؟‚ç‚جژ–ڈغ‚àپC‚ ‚é–ع‚ھڈo‚éژ–ڈغ‚ًژO‚آ•ھ‘«‚µ‚½ژ–ڈغ‚ئ‚ب‚ء‚ؤ‚¢‚é‚©‚ç‚إ‚·پD‚µ‚©‚µپCڈي‚ةپu“¯—l‚ةٹm‚©‚炵‚¢پv‚±‚ئ‚ھ•ھ‚©‚é‚ئ‚حŒہ‚è‚ـ‚¹‚ٌپD‚½‚ئ‚¦‚خ‘O‰ٌ‚جکb‚ة‚ ‚ء‚½‚و‚¤‚ب’¼•û‘ج‚جƒTƒCƒRƒچ‚جڈêچ‡پC–ع‚جڈo•û‚ھپu“¯—l‚ةٹm‚©‚炵‚¢پv‚©‚ح‚ي‚©‚è‚ـ‚¹‚ٌپD‚ذ‚ه‚ء‚ئ‚µ‚½‚çپu“¯—l‚ةٹm‚©‚炵‚¢پv‚©‚à‚µ‚ê‚ب‚¢‚ج‚إ‚·‚ھپC‚»‚¤‚إ‚ ‚é‚ئ”»’f‚إ‚«‚ب‚¢‚ب‚çژg‚ء‚ؤ‚ح‚¢‚¯‚ـ‚¹‚ٌپD
‡A‘S‚ؤ‚جژ–ڈغ‚ًچ‡‚ي‚¹‚é‚ئپCژژچs‘S‘ج‚جژ–ڈغ‚ً‘S•”•\‚¹‚é
‘Oڈq‚ج‚و‚¤‚ةپC‘S•”‚جژ–ڈغ‚ًچ‡‚ي‚¹‚½‚ئ‚«‚ةپCژژچs‘S‘ج‚ً•\Œ»‚إ‚«‚ؤ‚¢‚ب‚¢‚ئ‚¢‚¯‚ـ‚¹‚ٌپD‚و‚ء‚ؤپCپu‚P‚ھڈo‚éژ–ڈغپv‚ئپu‚Q‚ھڈo‚éژ–ڈغپv‚ج“ٌ‚آ‚جژ–ڈغ‚ًچl‚¦‚ؤپCپu‚P‚ھڈo‚éژ–ڈغپv‚ح1/2‚¾پI‚ئ‚حŒ¾‚¦‚ب‚¢‚ي‚¯‚إ‚·پDپu‚P‚ھڈo‚éژ–ڈغپv‚ئپu‚Q‚ھڈo‚éژ–ڈغپv‚¾‚¯‚إ‚حپCژژچs‘S‘ج‚ً•\Œ»‚إ‚«‚ؤ‚¢‚ب‚¢‚©‚ç‚إ‚·‚ثپD
‡B‚»‚ꂼ‚ê‚جژ–ڈغ‚جٹش‚إڈd‚ب‚ء‚ؤ‚¢‚é•”•ھ‚ھ‚ب‚¢
‚à‚µژژچs‘S‘ج‚ج‘ه‚«‚³‚ًŒvژZ‚·‚é‚ئ‚«‚ةپCٹـ‚ـ‚ê‚éژ–ڈغ‚ً“ٌڈd‚ةŒvژZ‚µ‚ؤ‚µ‚ـ‚¤‚ئپCژژچs‘S‘ج‚جگ³ٹm‚ب‘ه‚«‚³‚إ‚ح‚ب‚‚ب‚è‚ـ‚·پD‚½‚ئ‚¦‚خپCپu‚P‚©‚Q‚©‚R‚ھڈo‚éژ–ڈغپv‚ئپu‚Q‚©‚R‚©‚S‚ھڈo‚éژ–ڈغپv‚ئپu‚S‚©‚T‚©‚U‚ھڈo‚éژ–ڈغپv‚ئ‚¢‚¤ژO‚آ‚جژ–ڈغ‚ًچl‚¦‚ؤپCپu‚P‚©‚Q‚©‚R‚ھڈo‚éژ–ڈغپv‚جٹm—¦‚ح1/3‚إ‚·پI‚ئ‚حŒ¾‚¦‚ـ‚¹‚ٌپD
‚ب‚؛‚ب‚ç‚خپC‘S‘ج‚ً‘«‚µچ‡‚ي‚¹‚½‚ئ‚«‚ةپCپu‚Q‚ھڈo‚éژ–ڈغپvپu‚R‚ھڈo‚éژ–ڈغپvپu‚S‚ھڈo‚éژ–ڈغپv‚ً“ٌ‰ٌٹـ‚ٌ‚إ‚µ‚ـ‚ء‚ؤ‚¢‚é‚ج‚إپC‚±‚ê‚ç‚ً‘«‚µچ‡‚ي‚¹‚ؤ‚àپCژژچs‘S‘ج‚ج‘ه‚«‚³‚ًگ³ٹm‚ة“¾‚ç‚ê‚ب‚¢‚©‚ç‚ب‚ٌ‚إ‚·‚ثپD
‚³‚ؤپC‚±‚±‚إگV‚µ‚—pŒê‚ً“±“ü‚µ‚ـ‚·پC“ٌ‚آ‚جژ–ڈغ‚ھڈd‚ب‚ء‚ؤ‚¢‚ب‚¢پC‚ئ‚¢‚¤‚±‚ئ‚ًپC“ٌ‚آ‚جژ–ڈغ‚ھ”r‘¼“I‚إ‚ ‚éپC‚ئ‚¢‚¢‚ـ‚·پD‚±‚¤‚¢‚¤Œ¾—t‚ھ‚³‚ç‚ء‚ئژg‚¦‚é‚و‚¤‚ة‚ب‚é‚ئ‚ب‚ٌ‚©ƒJƒbƒR‚¢‚¢ٹ´‚¶‚ھ‚µ‚ـ‚¹‚ٌ‚©پI‚µ‚ب‚¢‚إ‚·‚و‚ثپI‚»‚¤‚إ‚·‚ثپI‚±‚¤‚¢‚¤Œ¾—t‚ً‚³‚ç‚ء‚ئژg‚¤‚ج‚حگ³’¼پC—Œn‚¾‚¯‚إ‚·پiڈخپj
‚±‚±‚ـ‚إ—ˆ‚ê‚خٹm—¦‚ح‚ظ‚ئ‚ٌ‚ا•ھ‚©‚ء‚½‚à“¯‘RپIپi‘½•ھ‚ثپIپjپD
‚ ‚ئڈd—v‚ب‚ج‚حپCٹm—¦‚جچ‡گ¬•”•ھ‚إ‚·پD“ٌ‚آ‚جƒTƒCƒRƒچ‚ًگU‚ء‚½ژ‚جٹm—¦‚ح‚ا‚¤‚ب‚é‚جپH‚ئ‚¢‚¤‚ئ‚±‚ë‚إ‚·‚ثپD‚؟‚ب‚ف‚ةپCˆê‚آ‚جƒTƒCƒRƒچ‚ًگU‚ء‚½ژ‚جٹm—¦‚ً‘«‚µچ‡‚ي‚¹‚éکb‚à‚ ‚è‚ـ‚·‚ھپCچ،‚ـ‚إ‚جگà–¾‚©‚ç‘ه‘ج‚»‚ج“ڑ‚¦‚حŒ©‚¦‚ؤ‚¢‚é‚©‚ئژv‚¢‚ـ‚·پD‚à‚؟‚ë‚ٌپC‚±‚ج“_‚àژں‰ٌپCˆêڈڈ‚ةگà–¾‚µ‚½‚¢‚ئژv‚¢‚ـ‚·پD
‚à‚¤ˆê“_ڈd—v‚ب‚ج‚حپCگ”‚¦ڈم‚°‚جŒّ—¦“I‚ب•û–@‚إ‚·‚ثپDƒTƒCƒRƒچ‚‚ç‚¢‚ب‚çٹب’P‚ةژ–ڈغ‚ًگ”‚¦‚ç‚ê‚ـ‚·‚ھپC‚à‚ء‚ئ•،ژG‚ة‚ب‚é‚ئ‘ه•د‚إ‚·پD‚»‚ج‚½‚ك‚جƒeƒNƒjƒbƒN‚ة‚آ‚¢‚ؤ‚à•×‹‚·‚é•K—v‚ھ‚ ‚è‚ـ‚·پD‹t‚ةŒ¾‚¦‚خپCچ‚چZگ”ٹwA‚إڈd—v‚ب‚ج‚حپC‚à‚¤‚»‚ج“ٌ‚آ‚‚ç‚¢‚µ‚©‚ب‚©‚ء‚½‚肵‚ـ‚·پiچ،‚جگV‰غ’ِ‚ئ‚©‚إ‚حگFپXˆل‚ء‚½‚è‚·‚é‚©‚à‚µ‚ê‚ب‚¢‚¯‚اپOپOپjپD
‚»‚ج•س‚ح‚à‚¤ڈ‚µگو‚إپI
‘±‚«پ@پثپ@ٹm—¦(5)ٹm—¦‚جچ‡گ¬
پyٹm—¦‚جچإگV‹Lژ–پz








‚±‚ج‹Lژ–‚ض‚جƒRƒپƒ“ƒg