分かりやすい高校数学:確率(10)期待値

前回　⇒　確率(9):区別なしの順列

十回目さー！ようやく！いや，もうサクサク行くっす．今日は期待値ですね．数学Aに期待値があったことを知ったのがつい最近というのは内緒です．

期待値で一番分かりやすいのはギャンブルです．今，ちょっとしたギャンブルを考えましょう．ギャンブル嫌いの人もちょっとお付き合いください（笑）

さて，サイコロを一回振って，もし６が出たら600円もらえるギャンブルがあるとします．ただし，もし６が出なかった場合は逆に150円払わなければなりません．さて，このギャンブル，やるべきかどうか？というのが問題です．さぁ，やるべきかやめるべきか．どちらだと思いますか？もちろん，ギャンブル嫌いだからやめるべき，というのは却下です（笑）

このギャンブルは，600円もらえるか，150円払うことになるかという二通りの結果しかありません．あなたがギャンブルをした時に，そのどちらになるかは結局神のみぞ知るです．だから神に聞いてください．以上！！！！・・・では数学になりませんね．ではどうやったら判断できるでしょうか？

この場合，自分が一人しかいないから難しくなってしまいます．運次第で，二通りの結果にしかならないですからね．ここでもし自分が１億人いるとしたら，全員がギャンブルやったときの結果を合わせて考えれば，このギャンブルが得なのか損なのかがはっきりしてきますね．

しかし，自分は一人しかいません．その場合どう考えるか！そう，自分を分解してしまえばいいのですっ！！！！！

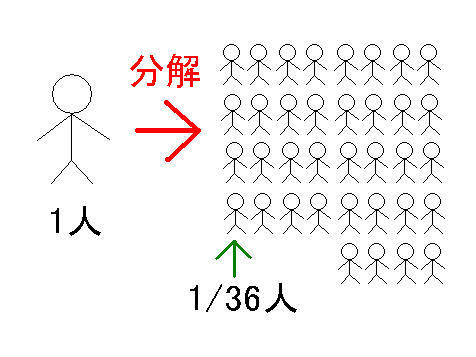
自分をたくさんの自分へと分解して，それぞれにギャンブルをやらせてあげたときの，その結果を集計すれば良いのです！！さて，実際にやってみましょう．

たくさんの自分がいた時に，ギャンブルに勝つ自分と，ギャンブルに負ける自分がどのくらいいるのかをまず考えます．サイコロで６が出れば勝ちなわけですから，その確率は1/6です．逆に負ける確率，６以外が出る確率は5/6です．つまり一人の自分を分解してギャンブルをやらせたら，1/6人はギャンブルに勝ち，5/6人はギャンブルに負けることになります．（自分の人数が，発生する確率と同じである点に注意してくださいね）

さて，ギャンブルに勝てば600円もらえるわけですから，ギャンブルで勝った総額は
　600円×1/6人＝100円　です．
一方，ギャンブルに負けた場合150円払うわけですから，ギャンブルに負けた総額は
　150円×5/6人＝125円　です．

よって，全員（といっても自分一人分ですが）のギャンブル結果の総額は，

100円（6が出た場合） - 125円（6以外が出た場合) ＝ -25円

負けてるー！！！損してるーーー！！つまり，このギャンブルをやると，25円損するということです．もちろんこれはあくまで，多数の自分がギャンブルを行った時の平均的な値です．実際に１回ギャンブルをしたら，600円もらえるか，150円失うかのどちらかしかありません．ただ，このギャンブルが損しやすいということは分かるわけです．

この-25円という値のことを，期待値と言います．つまり，一回のギャンブルで平均的に得られる結果のことを指します．

さて，期待値の一般的な計算方法について説明しましょう．基本的には先ほど示したように，

その結果で得られる値　×　分解した自分の人数

を，全員分足し合わせることで，期待値は得られます．ここで，自分を一人だとすると，先ほどの話の中で示したように，分解した自分の人数は，その事象の発生確率と同じです．よって，上の式を事象を使って書き換えると，

その事象で得られる値（ギャンブルの結果の金額）　×　その事象の発生確率（そのギャンブル結果になってしまった人数）

これを，全事象足し合わせたものと同じです．

◆ 付け足しメモ ◆

ちなみにたいていのギャンブルは期待値がマイナス，つまり損する計算になっています．宝くじなどは300円払って得られる金額の期待値は150円程度です．つまり買うごとに半額失うわけですね．もちろん運がよければ３億円手に入ることもあるのですが，あなたが平均的な運の持ち主であれば，半額損をするということになるわけです．

さて，これにて数学Ａの確率における基本部分の説明は終了です．もっと細かい話は色々あるわけですが，抑えておくべき重要な点だけを説明しています．他のことは，この考え方の流用でたいていなんとかなります．細かい部分を説明すればするほど，数学って分かりにくくなるように思うんですよね．ほんとに重要な点だけ説明すれば，あとの細かいことも理解しやすくなるし，とっつきやすくなるのでは，と思って書いています．

さて，この後何回かは，実際の問題に対してどう考えていけばいいかを，未説明の部分を交えて説明していきたいと思います．（もちろん，もっと細かい部分などを知りたい場合は，ほかのサイトを調べてみるのも良いと思います．ここで示した話を抑えておけば，理解しやすくなっているのではと期待しています（笑））

んーでも，その前に閑話休題を挟もうかなーとも思っています．お話として書きたいな～と思っていることがあるので・・・ま，そのへんはおいおい．

それではー．

数学ガール上を宣伝しておきながら，下をしていなかったので下に置いておきます．フィボナッチ数列とか，普段の生活で使わないよねーというようなお話でも，こういった形で見せられると興味を持っていけるのかな～と．数学の面白さに触れるには良いと思います．