分かりやすい高校数学:確率(7)順列
前回 ⇒ 確率(6)階乗!
七回目ー!!!ラッキーセブン!今回は,高校数学Aの確率で重要な「順列・組み合わせ」から,順列を勉強しますよー.
さて,とりあえずは,前回の疑問についてのお話です.忘れている方は前回のお話をもう一度ご覧下さいな.
それでは前回の疑問点を簡単にまとめましょう.
1~5までの数字が書かれた五個のボールから,二つ選んで並べる方法は何通りあるのか?という問題を考えると,その答えが,
5! (ボール全部) ÷ 3! (並べるのに使わなかった,余ったボール) = 5 × 4
と書けますよ!ということでした.さて,どうしてそう言えるのでしょうか???
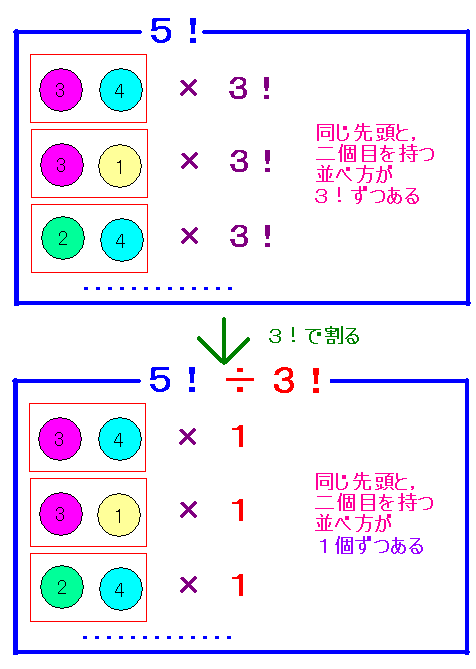
まず,この問題は,5個のボールを色々並べた時に,前二個の並べ方が何通りあるかを調べることと同じなのがおわかりでしょうか?5個のボールの中から二つ選んでいるわけですから,残りの三つは放置されています.これも一応並べてあげれば,5個のボールの並び方を考えるのと同じになりますよね.

ただし,5個のボールの並び方を考える場合と違う点は,残された三つのボールの並べ方は無視する必要がある点です.だって,もともとは放置されていたわけですから,並び方を気にする必要はないですよね.
つまり,5個のボールの並び方の数である5! に対して,後ろ三個のボールの並びを無視してあげることができれば,答えが得られる!!!ということになります.
もし,後ろ三個のボールの並び方を無視しないと,前二個のボールの並び方が同じものがたくさん出てきてしまいます.5個のボールの並べ方である5! は,全てのボールの並べ方を気にしているので,図のように,前二つが同じ並び方のものが複数個出てくるのですが,それはいったい何個でしょうか?

そう,図からわかるように,ボール三個の並べ方の数だけ出てきてしまいます.よって,3! 個です!
さて,5! の中には,前二個の並べ方が同じになっているものが3! ずつあります.ですので,5! を3! で割ってあげれば,重複が取り除かれ(後ろ三個のボールの並びが無視されて),それぞれ一個ずつ残ることになります.よって,5! ÷ 3! が答えになるんですね!!!!
さぁ,まとめましょう!!.ちょっとここでは数学らしく,数式でまとめてみましょう.数式といっても簡単なものですので,軽く構えていてください.
今,n個のボールがあった時に,そこからr個選んで並べる方法は何通りあるか?という問題を考えます.nとr はどんな整数でもいいですが,n個の中からr 個選ぶので,当然r はnより小さくないといけません.また,n個のボールからr 個のボールを選んで並べるわけですから,この時余ってしまったボールの数はn-r です.この時,問題の答えは,
n! (ボール全部の並べ方) ÷ (n-r )! (並び方を考える上で余ったボールの並べ方)
となります.公式という形になると覚えづらく感じる人も多いでしょう.実際,公式を単純に覚えるよりは,意味で覚えてしまったほうがいいと思います.ここで重要な点は,
全体の並べ方から,一部の並べ方を無視したいなら...
全体の並べ方を,無視したい部分の並べ方で割るんだぁ!!!
ということです.この考え方を覚えるようにしてください.この考え方は後の話でも使いますよ~.
さて,最後に一つ.今回の問題(全体から一部を抜き出して並べる時の並べ方の数)は,実は階乗と同じように,名前が付いています.それが「順列」です.
順列はnPr という形で表現されます.よって
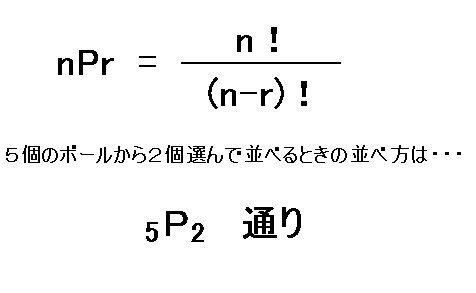
まー実際のところ,nPr はあんまり使いません(ぉい).それよりも次に話す,「組み合わせ」の方が重要です.この「組み合わせ」も,今回お話した考え方をちょっと応用するだけで簡単にできます.
そのお話は次回!!!!
次 ⇒ 確率(8)組み合わせ
七回目ー!!!ラッキーセブン!今回は,高校数学Aの確率で重要な「順列・組み合わせ」から,順列を勉強しますよー.
さて,とりあえずは,前回の疑問についてのお話です.忘れている方は前回のお話をもう一度ご覧下さいな.
それでは前回の疑問点を簡単にまとめましょう.
1~5までの数字が書かれた五個のボールから,二つ選んで並べる方法は何通りあるのか?という問題を考えると,その答えが,
5! (ボール全部) ÷ 3! (並べるのに使わなかった,余ったボール) = 5 × 4
と書けますよ!ということでした.さて,どうしてそう言えるのでしょうか???
まず,この問題は,5個のボールを色々並べた時に,前二個の並べ方が何通りあるかを調べることと同じなのがおわかりでしょうか?5個のボールの中から二つ選んでいるわけですから,残りの三つは放置されています.これも一応並べてあげれば,5個のボールの並び方を考えるのと同じになりますよね.
ただし,5個のボールの並び方を考える場合と違う点は,残された三つのボールの並べ方は無視する必要がある点です.だって,もともとは放置されていたわけですから,並び方を気にする必要はないですよね.
つまり,5個のボールの並び方の数である5! に対して,後ろ三個のボールの並びを無視してあげることができれば,答えが得られる!!!ということになります.
もし,後ろ三個のボールの並び方を無視しないと,前二個のボールの並び方が同じものがたくさん出てきてしまいます.5個のボールの並べ方である5! は,全てのボールの並べ方を気にしているので,図のように,前二つが同じ並び方のものが複数個出てくるのですが,それはいったい何個でしょうか?
そう,図からわかるように,ボール三個の並べ方の数だけ出てきてしまいます.よって,3! 個です!
さて,5! の中には,前二個の並べ方が同じになっているものが3! ずつあります.ですので,5! を3! で割ってあげれば,重複が取り除かれ(後ろ三個のボールの並びが無視されて),それぞれ一個ずつ残ることになります.よって,5! ÷ 3! が答えになるんですね!!!!
さぁ,まとめましょう!!.ちょっとここでは数学らしく,数式でまとめてみましょう.数式といっても簡単なものですので,軽く構えていてください.
今,n個のボールがあった時に,そこからr個選んで並べる方法は何通りあるか?という問題を考えます.nとr はどんな整数でもいいですが,n個の中からr 個選ぶので,当然r はnより小さくないといけません.また,n個のボールからr 個のボールを選んで並べるわけですから,この時余ってしまったボールの数はn-r です.この時,問題の答えは,
n! (ボール全部の並べ方) ÷ (n-r )! (並び方を考える上で余ったボールの並べ方)
となります.公式という形になると覚えづらく感じる人も多いでしょう.実際,公式を単純に覚えるよりは,意味で覚えてしまったほうがいいと思います.ここで重要な点は,
全体の並べ方から,一部の並べ方を無視したいなら...
全体の並べ方を,無視したい部分の並べ方で割るんだぁ!!!
ということです.この考え方を覚えるようにしてください.この考え方は後の話でも使いますよ~.
| ◆ 付け足しメモ ◆ さて,突然ですが,5個のボールから5個選んで並べる方法は何通りでしょうか? 5! ですよね~.このことを,今回の式に当てはめてみると, 5! (ボール全部の並べ方) ÷ 0! (並び方を考える上で余ったボールの並べ方) となります.この式が5! と等しいと考えると,0! = 1であるということになります.感覚的には0! は0でしょ?という人もいると思うのですが,ぶっちゃけこっちの方が扱いやすいので,数学では0! = 1となっています.そう決めてしまったわけですね. |
さて,最後に一つ.今回の問題(全体から一部を抜き出して並べる時の並べ方の数)は,実は階乗と同じように,名前が付いています.それが「順列」です.
順列はnPr という形で表現されます.よって
まー実際のところ,nPr はあんまり使いません(ぉい).それよりも次に話す,「組み合わせ」の方が重要です.この「組み合わせ」も,今回お話した考え方をちょっと応用するだけで簡単にできます.
そのお話は次回!!!!
次 ⇒ 確率(8)組み合わせ
【確率の最新記事】








この記事へのコメント