分かりやすい高校数学:確率(9)区別なしの順列

前回　⇒　確率(8):組み合わせ

９回目ー！！明らかに当初の予定通り（全１０回）いかない感じ爆発だけどサクサクいこー．

さて，今日は区別のつかないものが含まれている場合の順列です．たとえば，１０円玉３枚と５円玉２枚を並べる方法ですね．これも，基本的な考え方は変わりません．さーいってみよー．

いま，１０円玉３枚と５円玉２枚があるとします．これの並べ方は何通りでしょうか？ただし，１０円玉や５円玉は，それぞれの区別がつかないとします．書かれている製造年月日とかで区別はできなくて，１０円玉はどれも同じと考えるということです．

ここで重要なのは，１０円玉３枚は区別がつかないことです．よって仮に，１０円玉３枚を１０円玉Ａ，１０円玉Ｂ，１０円玉Ｃとつけたとします．このとき，

１０円玉Ａ，１０円玉Ｂ，１０円玉Ｃという並びと，
１０円玉Ａ，１０円玉Ｃ，１０円玉Ｂという並びは

区別つかない，つまり同じ並び方であると考えるわけです．

さぁ，これをどう解くのか．ここでもあの考え方が生かされます！！

全体の並べ方から，一部の並べ方を無視したいなら．．．

　全体の並べ方を，無視したい部分の並べ方で割るんだぁ！！！

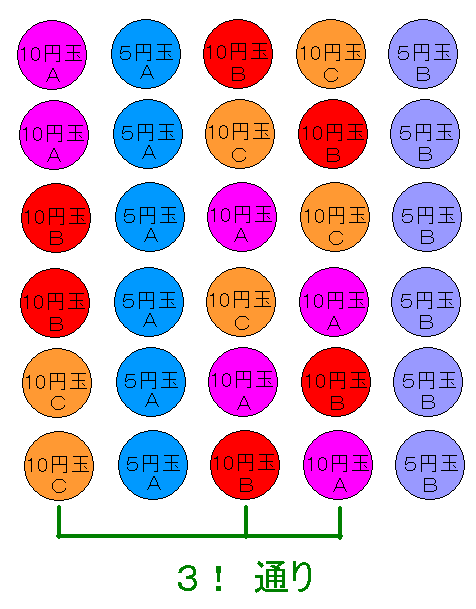
ここで無視したい並びは何か！１０円玉がどう並んでいても，無視して同じ並びだと考えたいわけですから，１０円玉の並べ方で割ってしまえば良いわけです．これによって，上の図にあるような3! 通りある並び方は，１０円玉の位置が変わらないので，同一であると見なせるようになります．（図では，１０円玉が１番目，３番目，４番目にありますが，これが１番目，４番目，５番目など，ほかの場合でも状況は変わりません．よって単純に3! で割ってあげてよいわけです）

同様に二枚ある５円玉の並び方でも割ってあげましょう．

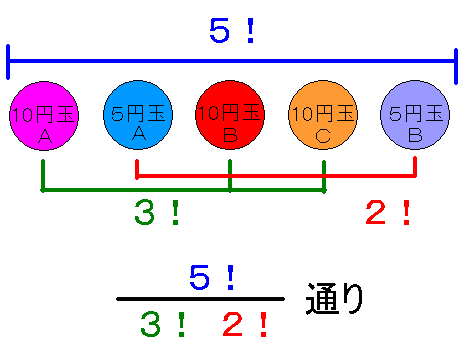
よって答えは，5! ÷ 3! ÷ 2!になります．

◆ 付け足しメモ ◆

この問題は，あくまで「順列」を求めていることに注意してください．「組み合わせ」の式と似ていますが，「組み合わせ」ではありません．

よって，「組み合わせ」の問題と合わせた問題を作ることもできます．たとえば，「１０円玉３枚と５円玉２枚から，２枚選ぶ方法は何通り？」などです．しかし，この問題は簡単には解けません．なぜなら，２枚選びだしたときに，１０円玉と５円玉が含まれている枚数が一定ではないため，それぞれの場合に分けて（１０円玉２枚を選びした場合，１０円玉１枚＋５円玉１枚を選びだした場合，５円玉２枚を選びだした場合の三通り）考えなければならないからです．（最初の問題の場合，対象としている並びの中に必ず１０円玉は３枚，５円玉が２枚入っていると決まっているので，3! と 2! とで割って問題ないのです．つまり，どんな状況でも割る数が変わらないから，場合わけしなくて良いのです．含まれる数が場合によって違うと，同じ数で割れなくなってしまうので，場合わけする必要があるんですね）

さて，あとは期待値のお話と，順列・組み合わせで飛ばしていた，細かい話をしていく予定です．やはり１０回で収まりませんが，まいっか．それではー．

数学ってどこで一番広く使われているかって言ったら，やはりコンピュータであるように思うのです．プログラムを作るためのプログラミングは，数学を知らなくてもできはするけど，知っていると知らないとでは大違いな面があります．そんな理解を助けてくれる本としてどうぞ．