分かりやすい高校数学:確率(番外1)大数の法則

前回　⇒　確率(12):実際の問題に対して(後編)

さて，今回のお話は「サイコロを沢山ふっているけど，最近１が出ていない！次は１がでやすいはず！」という考え方は正しいか？！という問題です．誰もが一度は疑問に思ったところではないかなと思うのですがどうでしょう．さて，本当に１が出ていないのなら，次は１が出やすくなるでしょうか？

これを考えるときに重要となるのは，それぞれの試行が独立であるかどうかです．本編の例の中であった，前日の気温とその次の日の気温などのように，独立性のないものの場合は，前日の気温（つまりは，それまでの結果）が次の日の気温（その次の結果）に影響します．

しかし，サイコロを振るという試行は独立となっています．これは，今までの試行結果（サイコロの出た目の状況）は，次の試行（次以降に出る目の種類）に一切影響を与えないということです．サイコロの目の出方は，前の結果に影響するはずないですよね．これは直感的にも理解できるかと思います．

よって，１が出やすくなるということはないのですが，それでも勘違いする人は少なくありません．これはなぜなのでしょうか？！

この勘違いを生み出しているのは，おそらく「１が出る確率は1/6」であるという事実ではないでしょうか？つまり，「たくさん実行した際に１が出る比率が1/6になるはずなのだから，1があんまり出てないなら，次からは1が出やすくなるはず！」というものです．

この思い込みは当然ながら間違っています．ではどこが間違っているのでしょうか？

それは，「１が出る比率を1/6にするためには，1をより多く出さなければいけない」という考え方です．そう，実際はそんなことはないのです．

それを例で示してみましょう．今，サイコロを15回振ったとき，各目の出た回数が，下のグラフに示すような内訳になったとします．

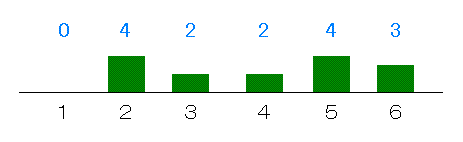
これによりますと，1が一度も出てきていません．出現する比率が0になっています．

さてそれでは，この後続けてサイコロを振ったときに，「１が出る比率を1/6にするためには，1をより多く出さなければいけない」という考え方をしなかった場合を考えて見ましょう．つまり，1を多く出そうとしないで考えてみます．

では何回ぐらい試行してみましょうか．そうですねー，どかんと３万回くらいやってみましょう！！！

理想的にサイコロが出たとすれば，それぞれの目が出る回数は3万回 ÷ ６＝ 5000回になります．そうすると下のような状況になります．

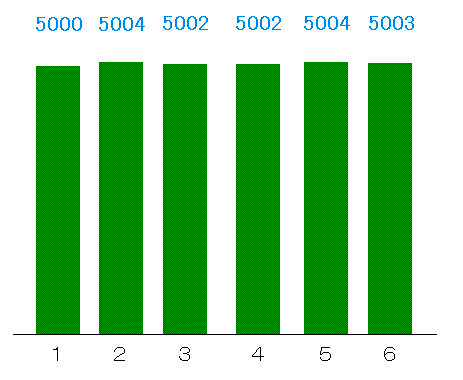
このとき，１が出た割合は5000 ÷ 30015 ≒ 0.1666 であり，1/6 = 1.666666・・・・なので，ほぼ1/6になっていることがわかります．

もうお分かりですね．小さな差が生まれたとしても，それよりはるかに多い量の試行を行えば，1/6になってしまうわけです．つまり，出現の比率を1/6に近づけられる理由は，それまでの試行結果から調整しているからではなく，もっと大量のデータで上書きしてしまうからなんですね．

なんかだまされたような気もするでしょうが，確率はあくまで大量のデータから導き出されるものです．小さなデータでは，あまり意味があるわけではないのです．

◆ 付け足しメモ ◆

ちなみに，大量の試行を行うとき，出現の比率（実際の試行のなかで１が出ている割合）が，発生する確率（１が出る確率）に近づくという性質のことを，大数の法則といいます．大数というほどに試行回数が大きいときに成立する性質ということですね．

大数の法則では，無限回試行した場合には出現比率と発生確率が一致する（正確に言えば，一致する確率が限りなく１に近づく）ということを示しています．ただし，無限回試行するということはできないことに注意してください．

どんなに多く試行しようとも，そこから一回でも試行すれば，さらに多い回数となってしまいます．よって，永遠に無限回試行へはたどり着けません．大数の法則では，無限回へと近づいていく状況を見てみると，どうみても出現比率と発生確率が一致する状況へ向かっているとしか思えないよ！といっているのであって，実際に無限回試行したときにどうなっているかは，誰にもわかりません．

さてさて，次回の予定なんですが，モンティ・ホール問題を扱いたいと思います．これは，あるテレビ番組で出題された問題であり，多くの人が答えを誤ったという近年有名な問題です．しかし，この問題を正確に理解することは難しく，さまざまなページで議論されていますが，万人を納得させるにはあまりいたっていないお話です．

モンティ・ホール問題のせいで，確率が良くわからなくなったという人も少なくないでしょう．実際，モンティ・ホール問題について，本来説明しなければならない点を説明していないことが多く，その状態で理解するのは困難ではないのかと感じていました．そんな問題をここで解決できるのかという疑念はありますが，間違いを恐れずにがんばって書いてみようかなと思っております（笑）

それでは～

数学の面白さを理解するっていうのは，なかなか難しい問題だなと，サイトを更新してきてつくづく思ったりしてます．どこで人の理解が止まってしまうのかを考えないと，説明できないんですよね．でも，その先にある面白さにたどり着ければ，数学に対する見方って劇的に変わっていくと思っています．