分かりやすい高校数学:確率(3)数え上げ
前回 ⇒ 確率(2)確率の基本
さて,非常に更新も遅れ気味になりながらも第三回目です.今日は確率はどのように数え上げで計算されるのか!ですね.
その前に軽くこれまでのおさらいをしましょう.
まず,確率とは「試行(サイコロを振る)を無限に行ったときに,目的とする事象(1が出る)が発生する割合」です.でも,それを実際に行うことはできません.無限に行うこと自体が不可能だからです.じゃあどうするんか!
結局のところ,無限ってのを「非常に大量な数」って考えてしまうとですね,「非常に大量に試行したとき,目的の事象がどのくらいの割合になるか」が確率となるわけです.
これを図で表してみます.

横の幅は,試行全体を表します.ここでは「無限と考えてもいいくらい非常に大量な数」の試行の結果を並べているものと考えてください.大量にあるので,この中には発生しうるすべての事象が含まれています.当然,目的とする事象である「1が出る」という事象も存在します.上の図では,その「1がでる」事象を水色で,残りの事象を青色で塗りつぶしています.
サイコロを振って1が出る確率とは,「大量にある試行の結果の中で,目的の事象の割合」と考えられるわけですから,上の四角の中で,水色で塗りつぶされた部分の割合であると分かります.
したがって,
(非常に大量な)試行の結果「1が出る」事象となった数 ÷ (非常に大量な)試行数
と計算できるわけです!
そうすると,じゃあ,どうやって(非常に大量な)試行数を計算するの!?ってなりますよね.やっぱりこれを実際にやるのは大変です.だからやりません!(笑).実際,その数自体はなくても計算できるんです.
確率の計算では,全体に対する「1が出る」割合が分かれば良く,試行の数は必ずしも必要ではないんです.つまり,試行数が分からずとも確率は計算できるわけです.そしてその方法の一つが数えあげなんですね.
じゃあ実際にどうすればいいのか.これは,「発生しうる事象同士の,発生割合の関係」をみるという方法を取ります.
具体的な例で追ってみましょう.先ほどの図では青い空白の部分は色々な事象が混ざっていましたが,「発生しうる事象」すべてをちゃんと書いてみます.

サイコロを振るという試行で「発生しうる事象」には,「1が出る」~「6が出る」という六種類があります.そのあとで,これらの「発生割合」(図でいう面積の広さ)の関係を考えてみるわけです.たとえば,「1が出る」事象と「2が出る」事象とで,発生割合の大きさはどちらがどのくらい大きいのか?などです.
これを調べる上で重要なのは,「サイコロは6つの数が書かれていますが,書かれている数字が違うだけで,それぞれの数字でサイコロの形が違うわけではない」点です.
これは下の図を見て説明しましょう.

左側に1と2の目がでたサイコロがあります.この二つはどこが違うのか?といえば,「面に書かれている数字が違うだけ」で,その他の部分に違いがありません.図のように,1の目のサイコロの数字を全部消して,2が上になるように書き換えてしまえば,もともとのサイコロで2が出た時の状態となんら変わりがありません.これによって,1の目が出ることも2の目が出ることも,サイコロの性質からは差がないことが分かります.
もしこれが下の図のように直方体のサイコロであった場合,1の目と2の目は形や大きさが違うため,数字を入れ替えた時に同じにはなりません.
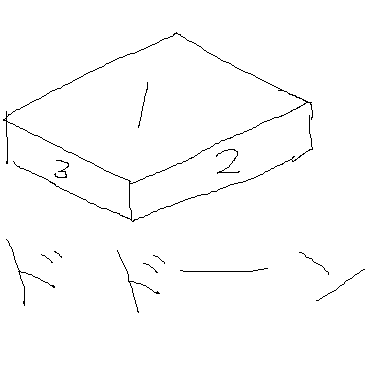
立方体のサイコロでは,1の目と2の目だけではなく,3~6の目に関しても同様に入れ替えが可能です.よって,「6つの目の出方に大差がない」ことが言えます.このことを,数学的には,「6つの目の出方は同様に確からしい」と言います.
さて,「6つの目の出方は同様に確からしい」ことが分かったことにより,それぞれの発生割合はほぼ等しいと見なせるようになります.そして,試行全体はこの六つの事象で表現できることから考えると,図のような状況になります.
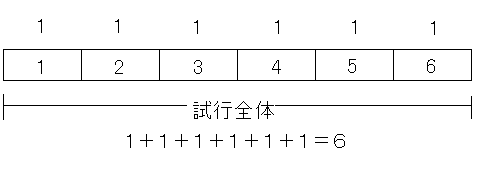
つまり,「1が出る」事象の大きさを1と考えたとき,2~6が出る事象はそれに等しいのですから,同様に1となります.試行全体はこの6つの足し合わせでできているわけですから,全体の大きさは6になります.
もうおわかりですね.「1が出る」事象の割合は,1/6となるわけです.このとき,分母の値(=全体の大きさ)は,発生しうる事象の数となっています.よって,前回説明した,目的の事象の数 ÷ 発生しうる事象の数 という計算によって確率が計算できていることも分かります.
ただし,目的の事象の数 ÷ 発生しうる事象の数 で計算できるのは,発生しうる事象がすべて,「同様に確からしい」場合だけです.たとえば先の図の中にありました,直方体のサイコロの場合,「同様に確からしい」とははっきり分かっていないので,この計算式を使うことはできません.このように,数え上げが使用できるかの条件には,ほかにもいくつかあります.
その条件については次回!
続き ⇒ 確率(4)数え上げの条件
BB塾

さて,非常に更新も遅れ気味になりながらも第三回目です.今日は確率はどのように数え上げで計算されるのか!ですね.
その前に軽くこれまでのおさらいをしましょう.
まず,確率とは「試行(サイコロを振る)を無限に行ったときに,目的とする事象(1が出る)が発生する割合」です.でも,それを実際に行うことはできません.無限に行うこと自体が不可能だからです.じゃあどうするんか!
結局のところ,無限ってのを「非常に大量な数」って考えてしまうとですね,「非常に大量に試行したとき,目的の事象がどのくらいの割合になるか」が確率となるわけです.
これを図で表してみます.
横の幅は,試行全体を表します.ここでは「無限と考えてもいいくらい非常に大量な数」の試行の結果を並べているものと考えてください.大量にあるので,この中には発生しうるすべての事象が含まれています.当然,目的とする事象である「1が出る」という事象も存在します.上の図では,その「1がでる」事象を水色で,残りの事象を青色で塗りつぶしています.
サイコロを振って1が出る確率とは,「大量にある試行の結果の中で,目的の事象の割合」と考えられるわけですから,上の四角の中で,水色で塗りつぶされた部分の割合であると分かります.
したがって,
(非常に大量な)試行の結果「1が出る」事象となった数 ÷ (非常に大量な)試行数
と計算できるわけです!
そうすると,じゃあ,どうやって(非常に大量な)試行数を計算するの!?ってなりますよね.やっぱりこれを実際にやるのは大変です.だからやりません!(笑).実際,その数自体はなくても計算できるんです.
確率の計算では,全体に対する「1が出る」割合が分かれば良く,試行の数は必ずしも必要ではないんです.つまり,試行数が分からずとも確率は計算できるわけです.そしてその方法の一つが数えあげなんですね.
じゃあ実際にどうすればいいのか.これは,「発生しうる事象同士の,発生割合の関係」をみるという方法を取ります.
具体的な例で追ってみましょう.先ほどの図では青い空白の部分は色々な事象が混ざっていましたが,「発生しうる事象」すべてをちゃんと書いてみます.
サイコロを振るという試行で「発生しうる事象」には,「1が出る」~「6が出る」という六種類があります.そのあとで,これらの「発生割合」(図でいう面積の広さ)の関係を考えてみるわけです.たとえば,「1が出る」事象と「2が出る」事象とで,発生割合の大きさはどちらがどのくらい大きいのか?などです.
これを調べる上で重要なのは,「サイコロは6つの数が書かれていますが,書かれている数字が違うだけで,それぞれの数字でサイコロの形が違うわけではない」点です.
これは下の図を見て説明しましょう.
左側に1と2の目がでたサイコロがあります.この二つはどこが違うのか?といえば,「面に書かれている数字が違うだけ」で,その他の部分に違いがありません.図のように,1の目のサイコロの数字を全部消して,2が上になるように書き換えてしまえば,もともとのサイコロで2が出た時の状態となんら変わりがありません.これによって,1の目が出ることも2の目が出ることも,サイコロの性質からは差がないことが分かります.
| ◆ 付け足しメモ ◆ |
もちろん,「数字が違う」という差はあるのですが,サイコロの目の出やすさに影響を与えるものではないため,差がないものとして考えます.そう,ここでは「目の出方(発生割合)に違いがあるか」ということに注目しているからなんですね. |
もしこれが下の図のように直方体のサイコロであった場合,1の目と2の目は形や大きさが違うため,数字を入れ替えた時に同じにはなりません.
立方体のサイコロでは,1の目と2の目だけではなく,3~6の目に関しても同様に入れ替えが可能です.よって,「6つの目の出方に大差がない」ことが言えます.このことを,数学的には,「6つの目の出方は同様に確からしい」と言います.
| ◆ 付け足しメモ ◆ |
ここで,同様に確か「らしい」と言っているのは,やっぱり正確に同じだ!とは言えないからなんです.サイコロに傷がついていたり,あるいはサイコロ表面に印刷した数字に使われてるインクの重さが違うだろ!とか,細かい形状の違いは言い出したらきりがないからなんです.だから,同様に確か「らしい」として,ほぼ同じ確率ですよー,ずれていても0.00001%とかいった,とっても小さな違いですよ~と表現しているわけです. |
さて,「6つの目の出方は同様に確からしい」ことが分かったことにより,それぞれの発生割合はほぼ等しいと見なせるようになります.そして,試行全体はこの六つの事象で表現できることから考えると,図のような状況になります.
つまり,「1が出る」事象の大きさを1と考えたとき,2~6が出る事象はそれに等しいのですから,同様に1となります.試行全体はこの6つの足し合わせでできているわけですから,全体の大きさは6になります.
もうおわかりですね.「1が出る」事象の割合は,1/6となるわけです.このとき,分母の値(=全体の大きさ)は,発生しうる事象の数となっています.よって,前回説明した,目的の事象の数 ÷ 発生しうる事象の数 という計算によって確率が計算できていることも分かります.
ただし,目的の事象の数 ÷ 発生しうる事象の数 で計算できるのは,発生しうる事象がすべて,「同様に確からしい」場合だけです.たとえば先の図の中にありました,直方体のサイコロの場合,「同様に確からしい」とははっきり分かっていないので,この計算式を使うことはできません.このように,数え上げが使用できるかの条件には,ほかにもいくつかあります.
その条件については次回!
続き ⇒ 確率(4)数え上げの条件
BB塾
【確率の最新記事】







この記事へのコメント