分かりやすい高校数学:確率(11)実際の問題に対して(前編)

前回　⇒　確率(10)期待値

今回と次回で確率の本編は終了です～．この回では実際の問題を解く上での話をしたいと思います．

実際に解く力を身につけるためには，数学Aの確率の問題をひたすら解く必要があります．問題のパターンってのは色々存在しているので，ひたすら解くことで，色々なパターンに慣れていかなければならないわけですね．

このサイトでもそれをやってみるかどうか迷ったのですが，別にここでやらなくても，問題に対する解答を分かりやすく説明しているサイトは沢山あります．

ただ，そういったサイトは，本当に大事なポイントだけを理解するのには不向きではないかと感じています．情報が多すぎるために，逆に分かりにくくなってしまっていないか，と思うわけですね．

なのでこのサイトでは，ポイントを絞ることで，数学を理解するきっかけになるようにしようと思いました．数学は複雑なようにみえて，実はシンプルな考え方の組み合わせでできていることが多いです．見かけの複雑さにとらわれて，くじけてしまう人も多いかと思います．その人たちの手助けとなるような，簡潔にポイントをおさえた話をしていくことにしました．

ここでは，確率などの問題を解く上での重要なポイントを説明していこうと思います．あくまで重要ポイントに限っています．この考え方をおさえておけば，問題を解くことはすぐにできなくても，解答の解説はすんなり理解できるようになるのではないかな～，そうなったらいいな～と思っておりますです．あれですよ，100点はとれなくとも平均点は取れるようになる位の感じです（笑）

さて，それではいってみましょうか．

順列・組み合わせで一番重要なことは，いかに問題を切り分けて考えるかです．全ての並びを計算する方法は説明してきましたが，実際の問題では部分部分になんらかの制約がある場合がほとんどです．その場合は，「制約がある部分とない部分に分けて計算し，最後に掛け合わせる」という方法を取ります．うまく切り分けられれば，分解した部分部分の並べ方を掛け合わせることで計算できます．（掛け算で組み合わせられるというのは，確率の考え方と同じです．異なる二つを組み合わせたいなら掛け合わせろ！ですね）

では実際に問題を解きながら考えてみましょう．

「１～９までの数字が書かれた９個のボールから５個選んで並べる際に，偶数が書かれたボールが２つ入っている並べ方は何通りか？」

一見すると順列の問題ですが，「偶数が書かれたボールが２つある」という制約が入っています．この場合は，「制約のある」偶数ボールと「制約のない」奇数ボールとで分けて考えるのです．

まず，偶数ボールは２，４，６，８と４個あるうちから２つ使うことになります．
よってその選び方は4C2=6通りですね．

一方，奇数ボールは１，３，５，７，９と５個あるうちから３つ使います．
よって，5C3=10通りですね．

ここで偶数ボールの選び方一つずつに対し，奇数ボールの選びかた(10通り)があるわけですから，偶数ボールを２つ含むボールの選び方は6×10=60通りとなります．

さらに，この段階では組み合わせを使って５個のボールを「選びだした」だけですので，これを並べる方法を考える必要があります．全体で５個あるボールを並べる方法は，5! ですよね！　

よって正解は，60 × 5! = 7200通となります．意外と多いですよね～．

ここでは「偶数」と「奇数」とで切り分けましたが，切り分ける方法はほかにも沢山あります．たとえば，偶数ボールの組み合わせを実際に「２，４」「２，６」「２，８」「４，６」「４，８」「６，８」と列挙して，それぞれの場合について計算することもできます．ただし，当然ながら計算が大変です．数学では，こうやって時間をかければたいていの問題は解けるのですが，時間がかかりすぎてはテストで良い点取れないわけですね．よって，いかに簡単に，楽をして計算できるか！が大切なんです（笑）

最初に述べた「いかに問題を切り分けて考えるか」というのは，「いかに時間がかからないように切り分けるか」という意味なんですね．そのためには特に，「制約のある部分だけ切りだす」ことが重要となります．

さて，もう一つ問題を考えてみましょう．

「１～９までの数字が書かれた９個のボールから５個選んで並べる際に，偶数が書かれたボールが２つ入っていて，しかも隣り合っている並べ方は何通りか？」

先ほどの問題に対し，さらに「隣り合っている」という条件が付きました．この制約をどこで切り分けるか！というのが問題となるわけですね．先ほどの問題では，「条件を満たすボールを選び出す」ところと，「選んだボールを並べる」という二つにも問題を切り分けています．ボールが隣り合うという条件は，後者にかかわる話なので，前者には関係ありません．よって，「条件を満たすボールを選び出す」方法は60通りのままで使えます．

一方で，ボールの並べ方ですが，ここでも偶数ボールだけに制約があります．なので，偶数ボールだけ特別視して考えます．

まず偶数ボールの並べ方は，2!通りありますね．

そして奇数ボールの並べ方を3! ・・・と考えられると良いのですが，そう簡単にはいきません．2! と 3! とを計算できても，その組み合わせ方法は，単純な掛け算では出てこないからです．先ほどのように組み合わせで考えているなら，別々にできますが，順列はお互いを混ぜて考える必要があるからですね．

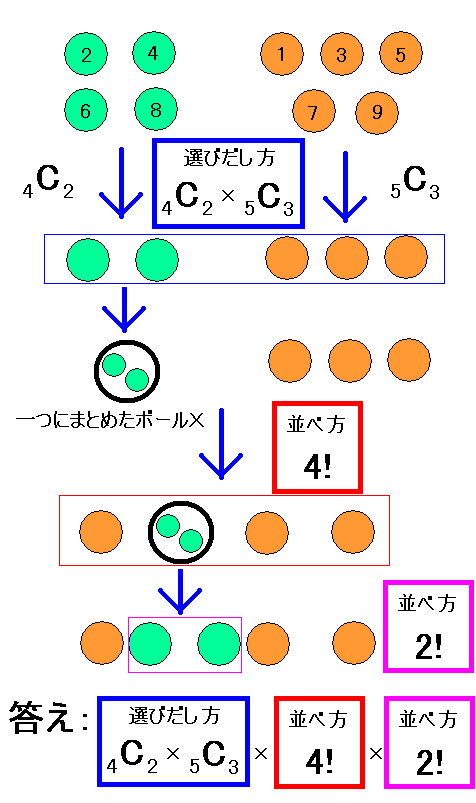
ではどうするのか．ここで偶数のボールは隣り合っているという条件に着目します．隣り合っているのならば，一つのボールと考えてしまってもよさそうですよね．そこで，偶数ボールをまとめた新しいボールＸを考えて，そのボールＸと奇数ボール３個のボールの並べ方を考えます．すると，並べ方はボール４個の並べ方なので，4! となります．もちろん，ボールＸの中にある偶数ボールの並べ方も考える必要があるので，全体の並べ方は4! × 2! ＝48通りとなります．

よって，問題の答えは，60 × 48 = 2880通りとなります．

隣り合うボールを一つにまとめて順列を考えるというのは，テクニックの一つです．この辺りは問題を解いて慣れていくしかないのですが，それより重要なのは，きっちりと問題を切り分けて考えることです！

◆ 付け足しメモ ◆

ちなみに，組み合わせを考える場合には，一つにまとめるというテクニックは使えません．まとめると，ボールが2つ分になってしまうため，組み合わせによってボールを８個選びだそうとしても，実は９個になっていたりするからです．

続きは後編で！文字数制限に引っ掛かったので（笑）

確率関係でお勧め本紹介ってことで．この本が良いなと思う点として，標準偏差の説明に力入れている点ですね．あれは結構使える概念なのに，学校での説明では何が良いのかさっぱりだったりするんですよね．ここでも説明してみたいとは思うのですが，まぁおいおい（笑）
あと，近年有名になっているベイズ理論についても書かれています．モンティ・ホール問題などで話題になった理論ですね．こちらのほうは近日このブログでも触れたいと思っています．