������₷�����Z���w:�m��(5)�m���̍���
�O��@�ˁ@�m��(4)�����グ�̏���
���āC�T��ځ[�I�I���\����Ă��܂����ˁD�\��ł͊m����S�\��ł�����Ȃ̂ŁC�������B���Ă��Ƃł��ˁD����́C�m���̍����ɂ��Ăł��D�������̎��ۂ�g�ݍ��킹�����̊m���́H���Ă̂��l���܂��D
������l����Ƃ��C���Ɖ���g�ݍ��킹��̂��ɂ���Čv�Z�̎d�����������܂��D��ʂ���ƈȉ��̓�ł��D
�@�������s���ʂ̒��̎��ۓ��m��g�ݍ��킹��
�A�ʂ̎��s���ʂ̎��ۂ�g�ݍ��킹��
�@�́C�Ⴆ�Έ�̃T�C�R����U�����Ƃ��ɁC�u�P���o��v�C�u�Q���o��v�Ƃ�����̎��ۂ�g�ݍ��킹���m���́H�Ƃ������̂ł��D����́C����܂ł̘b�̒��ł�����Ă��Ă܂��ˁD
����ɑ��A�́C�Ⴆ�u�T�C�R��������U�������ɁC���ڂ̎��s�̌��ʂ́u�P���o��v���ۂƂȂ�C���ڂ̎��s�́u�Q���o��v���ۂƂȂ�m���́H�Ƃ������̂ł��D����͇@�Ƃ͈Ⴄ���Ƃɒ��ӂ��Ă��������D�@���A���C�u�P���o��v�u�Q���o��v�Ƃ�����̎��ۂ�g�ݍ��킹�Ă��܂����C���ꂼ����������u���s�v���قȂ��Ă��܂��D�������ƂȂ��Ă���u���s�v�������Ȃ̂��C�Ⴄ�̂��Ōv�Z���Ⴄ��ł��ˁD
���Ă��āC�ł͂��ꂼ��̌v�Z���@���l���Ă݂܂��傤�D�܂��͇@����ł��ˁD
�Ƃ����Ă��C�@�͂��łɂ���Ă��Ă��܂��Ă��銴���ł��D�ړI�̎��ۂł����u�P���Q���o�鎖�ہv���C�u�P���o��v���ۂƁu�Q���o��v���ۂ�g�ݍ��킹�������i�������킹�����́j�ƍl���āC�ړI�̎��ۂ̐��@÷�@���������鎖�ۂ̐��@�̌v�Z������Ηǂ��킯�ł��D�����(1+1)/6 = 2/6 = 1/3�ł��ˁI
���Ă����ł�����Ǝ��_��ς��āC���ꂼ��̎��ۂ̊m���������킩���Ă��鎞�͂ǂ�������������l���Ă݂܂��傤�D���ɁC�u�P���o��v���ۂ̊m����1/6�C�u�Q���o��v���ۂ̊m����1/6���Ƃ��܂��D���āC���̎��́u�P���Q���o��v���ۂ̊m���́H
������1/6 + 1/6 = 2/6 = 1/3 �ƂȂ�܂��I����͊��o�I�ɂ�������₷�����ȂƁD��ق����ۂŌv�Z�����Ƃ�����𑫂��Ă����킯�ł�����C�m�����������Ⴆ�Ηǂ���ł��I
�������s�̎��ۂ������������Ȃ�C�m���𑫂����킹����I�I
�Ȃ������قɂȂ�܂������C�ɂ��Ȃ��ł������[���D����Ň@�̏ꍇ�ɂ��Ă̓o�b�`���ł��ˁI
���[�āC��������Ƃ��d�v�ȂƂ���ł���C�A�ɂ����Ă݂�[�D�Ƃ肠�����C�u�Q��T�C�R���U���āC���ꂼ��̃T�C�R���ɂ����āu�P���o��v�u�Q���o��v���g�ݍ��킹�ŋN����m���v���l���Ă݂܂��D
�P���ɓ�̃T�C�R���̑g�ݍ��킹���l���Ă݂�ƁC�}�̂悤�ɂȂ�܂��D��ڂ̃T�C�R���̖ڂɑ��C��ڂ̃T�C�R���̖ڂ��U��ނ��邩��C�S���łU×�U���R�U��ނ̉\�������邱�Ƃ�������܂��D�����āC���̒��Łu�P���o��v�u�Q���o��v�Ƃ������ۂ��g�ݍ��킳��ċN����̂́C�Q�ʂ�ł��D����āC�Q ÷ �R�U �� 1/18�@�ƌ����Ă����̂ł��傤���H�H�H
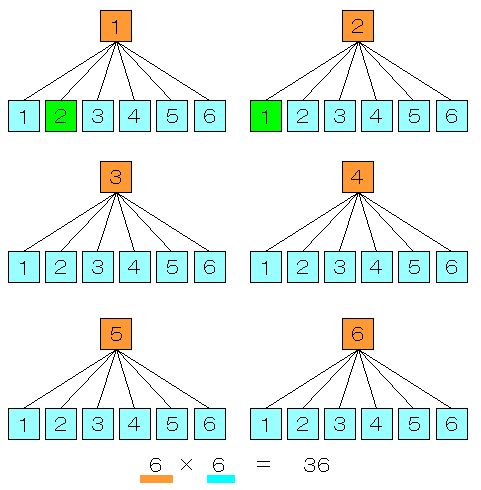
�����ŏd�v�Ȃ��Ƃ́C�����グ���S�R�U�̎��ۂ��C�����グ�̏��������Ă��邩�ǂ��������ɂȂ�܂��D�܂�C���̐}�̂悤�ɁC�Y���36�̗̈悪��������������Ă���Ȃ�C�����グ�ɂ��m���̌v�Z���ł���I�Ƃ������Ƃł��D

���̏����������߂ɂ́C�ȉ��̓�̏�������������Ă���Α��v�ł��D
1) ���������̎��s�������ۂ��C�����グ�̏��������Ă���D
2) ���������̎��s���Ɨ��ł���D
1)�̏����́C�����I�ɕ�����₷���ł���ˁD��̎��s��g�ݍ��킹�����ɏ������������Ȃ�C���̎��s�������������Ă�Ηǂ�����Ȃ��I�I�I���Ă��Ƃł��D������邱�ƂɗႦ�Č����C��̕���g�ݍ��킹���Y��ȕ�����肽���Ȃ�C���Ƃ����Y��ȓ��g�ݍ��킹��Ηǂ���ˁI���Ċ����ł��D���炻���C�t�ɕ�����ɂ������Ă�[�ȁi�j
�ł������ň�̋^�₪�����Ԑl������̂ł͂Ȃ��ł��傤���H����������C�l�Ԃ̋�����ƂɗႦ���ꍇ�ɁC�D�G�Ȑl�ƗD�G�Ȑl���ꏏ�Ɋ撣���Ă��C��l�̒�������������D�G�Ȍ��ʂɂȂ�Ȃ���������Ȃ������I�I�I�I
���Ől�ԂɗႦ��C���Đ������邩�Ǝv���܂����C���ۂɂ��̖��͊m���ŋN���肦���ł��ˁD�������C�m���̒��������킯�ł͂���܂��C���݂������݂��̏������ז����Ă��܂����Ƃ������ł��D���̎ז����N�����Ă��Ȃ�����Ă��Ƃ��m�F����̂��C2) ���������̎��s���Ɨ��ł���D�̏����Ȃ�ł��ˁD
���Ⴀ�C�Ɨ��ł�����Ăǂ��������ƂȂ̂ł��傤���H���́C���s�̒��ɂ́C�ق��̎��s�̌��ʂɉe������āC�m�����ς���Ă��܂����̂������ł��D����Ȃ��̂���̂��H���Ďv�������m��܂��C���R�̒��ł͕p�ɂɑ��݂��܂��D
���Ƃ��C����n��̖����̍ō��C���Ɩ�����̍ō��C���ł��D������̋C���́C�����̋C���ɉe������܂��D�����̍ō��C����30���������Ƃ��ɁC������̍ō��C����-5���ɂ��Ƃ͂܂��Ȃ��ł���ˁD�ł��C�����̍ō��C����0����������C������̍ō��C����-5���ł����������͂Ȃ��ł��D���̏ꍇ�C(30���E-5��)�Ƃ����g�ݍ��킹�͏o�ɂ����C(0���E-5��)�Ƃ����g�ݍ��킹�͏o�₷�����ƂɂȂ�܂��D���̂悤�ɁC�g�ݍ��킹���ɂ���ďo�₷���C�܂�m�����ς���Ă��Ă��܂��Ă���킯�ł��D����́C�����グ�ɂ����ĂƂĂ��ז��ɂȂ�܂��D���������������������Ȃ����Ƃ��u�Ɨ��ł����v�Ƃ����̂ł��D
�Ɨ��łȂ��ꍇ���T�C�R���ɗႦ��ƁC���̐}�̂悤�ɂȂ�܂��D�܂�C��ڂ̃T�C�R���̖ڂɂ���āC��ڂ̃T�C�R���̏o�����ς���Ă��܂��킯�ł��ˁD
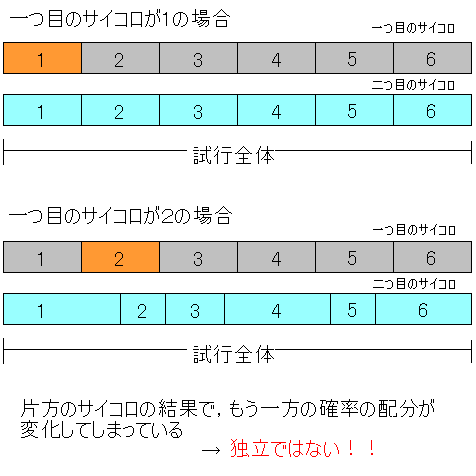
�ʏ�C���ݒ�̒��ŁC�Ɨ��ł��邩�Ȃ����͖��m�ɏ�����Ă��܂����C�����ĂȂ��Ă��T�C�R���̎��s�͓Ɨ��ƌ��Ȃ��đ��v�ł��D���ۊ��o�I�ɁC��̊ԂɊW�͂Ȃ��Ǝv����ł��傤�H
���āC������̏��������̏ꍇ��������Ă���킯�ł�����C���߂����m����1/18�ł���ƌ�����킯�ł��D�����l�ł����[�D
���Ȃ݂ɁC�m�����������Ă���ꍇ�͂ǂ��Ȃ�ł��傤���H�܂�C�u�P���o��v�m����1/6�C�u�Q���o��v�m����1/6�ƕ������Ă����Ԃ���v�Z����ꍇ�ł��D
�m���̏ꍇ�́C��قǏq�ׂ���̏����̂����̈�ڂ͊W����܂���D����������グ�̏���������ł��D�������C��ڂ̏����͂�������Ă��܂��D�m���ł��C�Ɨ��ł��邩�͋C�ɂ��Ȃ��Ă͂����܂���D
��̎��s���Ɨ��ł���C����|�����킹�邱�ƂŊm���̍������ł��܂��D������C���o�I�ɕ�����₷���ł���ˁD�����グ�̎����e���ۂ��|�����킹��(6×6=36)�C�v�Z���Ă����킯�ł�����D����āC�u�P���o��v�u�Q���o��v��g�ݍ��킹���m����1/6 * 1/6 =1/36�ƂȂ�܂��D
�ʂ̎��s�̎��ۂ������������Ȃ�C�m�����|�����킹����I�I
���ق͗�ɂ���ċC�ɂ��Ȃ��ł������[���D
������������Ƒ҂��āI���ꂾ���ł́u1��ڂ�1���o�āC2��ڂ�2���ł�v�ꍇ�����Ȃ̂ŁC�u1��ڂ�2���o�āC2��ڂ�1���ł�v�ꍇ���l���Ă��܂����D���̓��g�ݍ��킹��ɂ͂ǂ���������̂��E�E�E�E�H�I�����C��Ƃ��������s����o�Ă�����̂ł�����C�������킹��悢�̂ł��I�I�I
����āC�u1��ڂ�1���o�āC2��ڂ�2���ł�v�m��1/6 �ƁC�u1��ڂ�2���o�āC2��ڂ�1���ł�v�m��1/6�𑫂����킹�āC1/36+1/36=2/36=1/18�ƂȂ�܂��D�����Ɛ����グ�̏ꍇ�ƈ�v���܂����ˁ[�D
���āC�m���Ɋւ��Ă͑唼�I�����܂����D���Ƃ͐����グ�̕��@�ł��ˁD�����グ�ɂ́C�K��C����C�g�ݍ��킹�Ȃǂ���܂����C�d�v�ȓ_�͂Q���炢�ł��D���̂Q�_�𗝉����Ă��܂��C�X���[�Y�ɍs���Ǝv���܂��I�����I
����͂��̂Q�_�ɂ��Ă��b���܂���[�D���ł́D
���@�ˁ@�m��(6)�K��
���āC�T��ځ[�I�I���\����Ă��܂����ˁD�\��ł͊m����S�\��ł�����Ȃ̂ŁC�������B���Ă��Ƃł��ˁD����́C�m���̍����ɂ��Ăł��D�������̎��ۂ�g�ݍ��킹�����̊m���́H���Ă̂��l���܂��D
������l����Ƃ��C���Ɖ���g�ݍ��킹��̂��ɂ���Čv�Z�̎d�����������܂��D��ʂ���ƈȉ��̓�ł��D
�@�������s���ʂ̒��̎��ۓ��m��g�ݍ��킹��
�A�ʂ̎��s���ʂ̎��ۂ�g�ݍ��킹��
�@�́C�Ⴆ�Έ�̃T�C�R����U�����Ƃ��ɁC�u�P���o��v�C�u�Q���o��v�Ƃ�����̎��ۂ�g�ݍ��킹���m���́H�Ƃ������̂ł��D����́C����܂ł̘b�̒��ł�����Ă��Ă܂��ˁD
����ɑ��A�́C�Ⴆ�u�T�C�R��������U�������ɁC���ڂ̎��s�̌��ʂ́u�P���o��v���ۂƂȂ�C���ڂ̎��s�́u�Q���o��v���ۂƂȂ�m���́H�Ƃ������̂ł��D����͇@�Ƃ͈Ⴄ���Ƃɒ��ӂ��Ă��������D�@���A���C�u�P���o��v�u�Q���o��v�Ƃ�����̎��ۂ�g�ݍ��킹�Ă��܂����C���ꂼ����������u���s�v���قȂ��Ă��܂��D�������ƂȂ��Ă���u���s�v�������Ȃ̂��C�Ⴄ�̂��Ōv�Z���Ⴄ��ł��ˁD
| �� �t���������� �� ���Ȃ݂ɁC��̃T�C�R������U��̂ł͂Ȃ��C�����ɐU�����Ƃ��Ă��A�Ɠ����l�����ɂȂ�܂��D���ڂ̃T�C�R����U���Ă���C���ڂ̃T�C�R����U��܂ł̎��Ԃ��O�ɂȂ��������ŁC���ꂼ��́u���s�v���ς���Ă���킯�ł͂Ȃ�����ł��D �������C�u��̃T�C�R����U��v�Ƃ����C���̎��s���l���邱�Ƃ��ł��܂��D�������C���̎��s���琶�܂�鎖�ۂ͕��G�ɂȂ�C�u���l�Ɋm���炵���v������������̂���ςɂȂ�܂��D�܂�C�����̃T�C�R����U���Ă݂��̂Ɠ����悤�ȏɂȂ��Ă��܂��C�����グ�ɂ��m���v�Z����ςɂȂ��ł��ˁD�Ȃ̂ŁC�ʏ�͂��ꂼ��̎��s�ɕ����čl���܂��D�܁[�����������C�ʁX�ɍl���������y������ʁX�ɍl���܂��I���Ċ����ł��D �܂����R�Ȃ���C�T�C�R���ƃR�C���𓊂��Ă݂āC�T�C�R���Łu�P���o��v�Ƃ������ۂƁC�R�C���Łu�\���o��v�Ƃ������ۂƂ�g�ݍ��킹��ꍇ�͇A�̕��@�ōl���܂��D�u���s�v���قȂ��Ă��邩��ł��ˁD |
���Ă��āC�ł͂��ꂼ��̌v�Z���@���l���Ă݂܂��傤�D�܂��͇@����ł��ˁD
�Ƃ����Ă��C�@�͂��łɂ���Ă��Ă��܂��Ă��銴���ł��D�ړI�̎��ۂł����u�P���Q���o�鎖�ہv���C�u�P���o��v���ۂƁu�Q���o��v���ۂ�g�ݍ��킹�������i�������킹�����́j�ƍl���āC�ړI�̎��ۂ̐��@÷�@���������鎖�ۂ̐��@�̌v�Z������Ηǂ��킯�ł��D�����(1+1)/6 = 2/6 = 1/3�ł��ˁI
���Ă����ł�����Ǝ��_��ς��āC���ꂼ��̎��ۂ̊m���������킩���Ă��鎞�͂ǂ�������������l���Ă݂܂��傤�D���ɁC�u�P���o��v���ۂ̊m����1/6�C�u�Q���o��v���ۂ̊m����1/6���Ƃ��܂��D���āC���̎��́u�P���Q���o��v���ۂ̊m���́H
������1/6 + 1/6 = 2/6 = 1/3 �ƂȂ�܂��I����͊��o�I�ɂ�������₷�����ȂƁD��ق����ۂŌv�Z�����Ƃ�����𑫂��Ă����킯�ł�����C�m�����������Ⴆ�Ηǂ���ł��I
�������s�̎��ۂ������������Ȃ�C�m���𑫂����킹����I�I
�Ȃ������قɂȂ�܂������C�ɂ��Ȃ��ł������[���D����Ň@�̏ꍇ�ɂ��Ă̓o�b�`���ł��ˁI
| �� �t���������� �� ���Ȃ݂ɁC���̌v�Z���Ɏg�p����m�����C�����グ�Ōv�Z���ꂽ���̂łȂ��Ă���肠��܂���D�����グ�͊m�����v�Z���邽�߂̈��@�ł����Ȃ����Ƃ͒��ӂ��Ă��������D���ɂ��m�������߂���@�͂���킯�ł��D |
���[�āC��������Ƃ��d�v�ȂƂ���ł���C�A�ɂ����Ă݂�[�D�Ƃ肠�����C�u�Q��T�C�R���U���āC���ꂼ��̃T�C�R���ɂ����āu�P���o��v�u�Q���o��v���g�ݍ��킹�ŋN����m���v���l���Ă݂܂��D
�P���ɓ�̃T�C�R���̑g�ݍ��킹���l���Ă݂�ƁC�}�̂悤�ɂȂ�܂��D��ڂ̃T�C�R���̖ڂɑ��C��ڂ̃T�C�R���̖ڂ��U��ނ��邩��C�S���łU×�U���R�U��ނ̉\�������邱�Ƃ�������܂��D�����āC���̒��Łu�P���o��v�u�Q���o��v�Ƃ������ۂ��g�ݍ��킳��ċN����̂́C�Q�ʂ�ł��D����āC�Q ÷ �R�U �� 1/18�@�ƌ����Ă����̂ł��傤���H�H�H
�����ŏd�v�Ȃ��Ƃ́C�����グ���S�R�U�̎��ۂ��C�����グ�̏��������Ă��邩�ǂ��������ɂȂ�܂��D�܂�C���̐}�̂悤�ɁC�Y���36�̗̈悪��������������Ă���Ȃ�C�����グ�ɂ��m���̌v�Z���ł���I�Ƃ������Ƃł��D
���̏����������߂ɂ́C�ȉ��̓�̏�������������Ă���Α��v�ł��D
1) ���������̎��s�������ۂ��C�����グ�̏��������Ă���D
2) ���������̎��s���Ɨ��ł���D
1)�̏����́C�����I�ɕ�����₷���ł���ˁD��̎��s��g�ݍ��킹�����ɏ������������Ȃ�C���̎��s�������������Ă�Ηǂ�����Ȃ��I�I�I���Ă��Ƃł��D������邱�ƂɗႦ�Č����C��̕���g�ݍ��킹���Y��ȕ�����肽���Ȃ�C���Ƃ����Y��ȓ��g�ݍ��킹��Ηǂ���ˁI���Ċ����ł��D���炻���C�t�ɕ�����ɂ������Ă�[�ȁi�j
�ł������ň�̋^�₪�����Ԑl������̂ł͂Ȃ��ł��傤���H����������C�l�Ԃ̋�����ƂɗႦ���ꍇ�ɁC�D�G�Ȑl�ƗD�G�Ȑl���ꏏ�Ɋ撣���Ă��C��l�̒�������������D�G�Ȍ��ʂɂȂ�Ȃ���������Ȃ������I�I�I�I
���Ől�ԂɗႦ��C���Đ������邩�Ǝv���܂����C���ۂɂ��̖��͊m���ŋN���肦���ł��ˁD�������C�m���̒��������킯�ł͂���܂��C���݂������݂��̏������ז����Ă��܂����Ƃ������ł��D���̎ז����N�����Ă��Ȃ�����Ă��Ƃ��m�F����̂��C2) ���������̎��s���Ɨ��ł���D�̏����Ȃ�ł��ˁD
���Ⴀ�C�Ɨ��ł�����Ăǂ��������ƂȂ̂ł��傤���H���́C���s�̒��ɂ́C�ق��̎��s�̌��ʂɉe������āC�m�����ς���Ă��܂����̂������ł��D����Ȃ��̂���̂��H���Ďv�������m��܂��C���R�̒��ł͕p�ɂɑ��݂��܂��D
���Ƃ��C����n��̖����̍ō��C���Ɩ�����̍ō��C���ł��D������̋C���́C�����̋C���ɉe������܂��D�����̍ō��C����30���������Ƃ��ɁC������̍ō��C����-5���ɂ��Ƃ͂܂��Ȃ��ł���ˁD�ł��C�����̍ō��C����0����������C������̍ō��C����-5���ł����������͂Ȃ��ł��D���̏ꍇ�C(30���E-5��)�Ƃ����g�ݍ��킹�͏o�ɂ����C(0���E-5��)�Ƃ����g�ݍ��킹�͏o�₷�����ƂɂȂ�܂��D���̂悤�ɁC�g�ݍ��킹���ɂ���ďo�₷���C�܂�m�����ς���Ă��Ă��܂��Ă���킯�ł��D����́C�����グ�ɂ����ĂƂĂ��ז��ɂȂ�܂��D���������������������Ȃ����Ƃ��u�Ɨ��ł����v�Ƃ����̂ł��D
�Ɨ��łȂ��ꍇ���T�C�R���ɗႦ��ƁC���̐}�̂悤�ɂȂ�܂��D�܂�C��ڂ̃T�C�R���̖ڂɂ���āC��ڂ̃T�C�R���̏o�����ς���Ă��܂��킯�ł��ˁD
�ʏ�C���ݒ�̒��ŁC�Ɨ��ł��邩�Ȃ����͖��m�ɏ�����Ă��܂����C�����ĂȂ��Ă��T�C�R���̎��s�͓Ɨ��ƌ��Ȃ��đ��v�ł��D���ۊ��o�I�ɁC��̊ԂɊW�͂Ȃ��Ǝv����ł��傤�H
| �� �t���������� �� ���ۂɓ�̎��s���Ɨ��ł��邩�f����̂͊ȒP�ł͂Ȃ��ł��D������ƓƗ��ł��邩�ׂ�Ȃ�C���ʂ̎��s���s���ē��v�I�Ȍ�������{����K�v������܂��D���Z���w�ł͂����܂ł�邱�Ƃ͂Ȃ��C�T�C�R����U�鎎�s��R�C���𓊂��ė��\�����鎎�s�Ȃǂ́C���ꂼ��Ɨ�����`�Ƃ����Öق̗����ɏ]���čl���Ă��܂��D �܂��C�Ɨ��łȂ��ꍇ�̊m���͂ǂ��v�Z����̂��C�Ƃ������ƂɊւ��ẮC�ȒP�Ɍ����C�S�������čl���܂��D�܂�C��ڂ̃T�C�R�����P�ł���ꍇ�ƂQ�ł���ꍇ�C���邢�͂R�C�S�C�T�C�U�ł���ꍇ���ꂼ����l���āC�m�����v�Z���Ă����Ƃ����C�ƂĂ��ʓ|�ȍ�Ƃ�����킯�ł��D |
���āC������̏��������̏ꍇ��������Ă���킯�ł�����C���߂����m����1/18�ł���ƌ�����킯�ł��D�����l�ł����[�D
���Ȃ݂ɁC�m�����������Ă���ꍇ�͂ǂ��Ȃ�ł��傤���H�܂�C�u�P���o��v�m����1/6�C�u�Q���o��v�m����1/6�ƕ������Ă����Ԃ���v�Z����ꍇ�ł��D
�m���̏ꍇ�́C��قǏq�ׂ���̏����̂����̈�ڂ͊W����܂���D����������グ�̏���������ł��D�������C��ڂ̏����͂�������Ă��܂��D�m���ł��C�Ɨ��ł��邩�͋C�ɂ��Ȃ��Ă͂����܂���D
��̎��s���Ɨ��ł���C����|�����킹�邱�ƂŊm���̍������ł��܂��D������C���o�I�ɕ�����₷���ł���ˁD�����グ�̎����e���ۂ��|�����킹��(6×6=36)�C�v�Z���Ă����킯�ł�����D����āC�u�P���o��v�u�Q���o��v��g�ݍ��킹���m����1/6 * 1/6 =1/36�ƂȂ�܂��D
�ʂ̎��s�̎��ۂ������������Ȃ�C�m�����|�����킹����I�I
���ق͗�ɂ���ċC�ɂ��Ȃ��ł������[���D
������������Ƒ҂��āI���ꂾ���ł́u1��ڂ�1���o�āC2��ڂ�2���ł�v�ꍇ�����Ȃ̂ŁC�u1��ڂ�2���o�āC2��ڂ�1���ł�v�ꍇ���l���Ă��܂����D���̓��g�ݍ��킹��ɂ͂ǂ���������̂��E�E�E�E�H�I�����C��Ƃ��������s����o�Ă�����̂ł�����C�������킹��悢�̂ł��I�I�I
����āC�u1��ڂ�1���o�āC2��ڂ�2���ł�v�m��1/6 �ƁC�u1��ڂ�2���o�āC2��ڂ�1���ł�v�m��1/6�𑫂����킹�āC1/36+1/36=2/36=1/18�ƂȂ�܂��D�����Ɛ����グ�̏ꍇ�ƈ�v���܂����ˁ[�D
| �� �t���������� �� ����́C�u�T�C�R������U��v�ꍇ���l�����킯�ł����C���ꂪ�u�T�C�R�����j�����ɐU��v�ꍇ�ł��v�Z�͕ς��܂���D ������ɐU��ƁC�ǂ������ǂ����̃T�C�R������ʂ��Ȃ��Ȃ邩��C�u�P���o��v�Ɓu�Q���o��v�Ƃ������ۂ̑g�ݍ��킹�͂P�����Ȃ��̂ł́H�ƍl����l�����܂����C�����グ�ŏd�v�Ȃ̂͂����܂ŁC�u���ׂĂ̎��ۂ����l�Ɋm���炵�����Ɓv�ł��D����͎��������T�C�R���̋�ʂ������邩�ǂ����ɊW�͂���܂���D�������ɂ͋�ʂ��Ȃ��������āC���ꂼ��̃T�C�R���́u���l�Ɋm���炵���v�U�̎��ۂ�g�ݍ��킹�čl����K�v������킯�ł�����C��̃T�C�R���͋�ʂ������̂Ƃ��čl����K�v������܂��D |
���āC�m���Ɋւ��Ă͑唼�I�����܂����D���Ƃ͐����グ�̕��@�ł��ˁD�����グ�ɂ́C�K��C����C�g�ݍ��킹�Ȃǂ���܂����C�d�v�ȓ_�͂Q���炢�ł��D���̂Q�_�𗝉����Ă��܂��C�X���[�Y�ɍs���Ǝv���܂��I�����I
����͂��̂Q�_�ɂ��Ă��b���܂���[�D���ł́D
���@�ˁ@�m��(6)�K��
�y�m���̍ŐV�L���z







���̋L���ւ̃R�����g