分かりやすい高校数学:確率(番外2)モンティ・ホール問題1
前回 ⇒ 確率(番外1):大数の法則
今日は最近有名な確率の問題として知られている,モンティ・ホール問題についてです.この問題についての議論をすると,正解は知られているのにそれでも納得のいかない人が現れたりする問題であり,正確な理解にたどり着くのが難しい問題として知られています.
今回はそれを分かりやすく説明していきたいと思いますが,なにぶん難しい問題ではあるんで,誤解を恐れずに自分なりの解釈で説明していきたいと思います.(なので,微妙に間違ってるかも(笑))
さて,それではモンティ・ホール問題とは何か?から行ってみましょう.下に,Wikipediaで示されている問題文を抜粋しています.
「プレイヤー(解答者)の前に3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろにはヤギ(はずれを意味する)がいる。プレイヤーは新車のドアを当てると新車がもらえる。プレイヤーが1つのドアを選択した後、モンティ(司会者)が残りのドアのうちヤギがいるドアを開けてヤギを見せる。
ここでプレイヤーは最初に選んだドアを、残っている開けられていないドアに変更しても良いと言われる。プレイヤーはドアを変更すべきだろうか?
問題のルール:
(1) 3つのドア (A, B, C) に(景品、ヤギ、ヤギ)がランダムに入っている。
(2) プレイヤーはドアを1つ選ぶ。
(3) モンティは残りのドアのうち1つを必ず開ける。
(4) モンティの開けるドアは、必ずヤギの入っているドアである。
(5) モンティはプレーヤーにドアを選びなおしてよいと必ず言う。 」
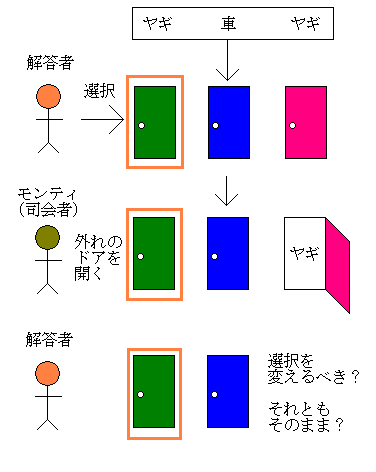
さぁ,答えはおわかりでしょうか?
ま,いきなり答えを言ってしまいますと,ドアを変更した方が良い,となります.最初に選択したドアに新車がある確率は1/3であり,変更した先のドアにある確率は2/3なんです.
この解答に対し,多くの人が疑問を唱えたのです.どっちも同じ1/2じゃないのか?と言ったわけですね.
あなたはどちらが正しいと思ったでしょうか?
さて,問題をシンプルに考えてみましょう.最初に一つ選んだときに,正解である確率は1/3です.これはいいですね.
その後で,モンティが不正解のドアを一つ開けます.この行動によって,確率が変わっているわけです.つまり,開けることによって消えた1/3の確率分がどこへ行くのか,という話になります.
これが全て,選択していないドアに割り振られたら2/3になります(図の(1)),
残り二つのドアに平等に割り振られれば,1/2になるわけです(図の(2)).
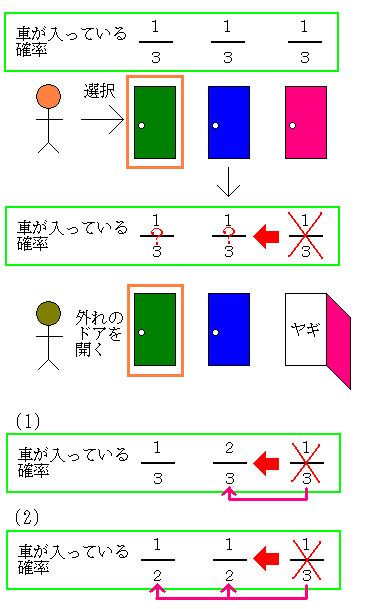
この割り振りが,どういう計算によって導かれるのかについては,次回以降においておきます.ここではその前に,なぜ,二通りの意見が生まれてきてしまうのかを考えたいと思います.その原因はなんなのでしょうか?
じつは,その原因は非常に根本的な部分にあります.
それは,「そもそも,この問題の答えって確率で計算できるの?」という点です.
だって考えてみてください.この問題,司会者であるモンティは正解を知っています.でなければ,不正解のドアを開けることができません.解答者が「このドアが正解である確率は2/3だ!」って言っているよこで,モンティは「いや,そっちは不正解だから.見当違いだねー」と思っているわけです.つまり,司会者からしてみれば,確率の問題ではなく,厳然たる事実なわけです.
これまで説明してきたサイコロの問題では,確率が1/6というのは誰にとっても同じでした.「このサイコロは次に振ったとき,1が出るのさ!」と分かっている人はいないわけです.
なにやら,おかしな感じがしてきていませんか?実はこの不整合さが,問題をややこしくしているんです.
そう,この不整合さはどうして生じているのか,その答えをお教えしましょう.
実は,確率は二種類存在するんです!!!!!
そう.モンティ・ホール問題で問われている「確率」と,今まで学習してきた,サイコロの出る目の確率などの指す「確率」は,似て非なるものなんです.
サイコロの出る目の「確率」などは,誰の目から見ても同じである事実を指しています.このような客観性を持っている確率のことを「客観確率」と言います.
しかし,モンティ・ホール問題の指す確率はそうではありません.司会者と解答者とでは見ている確率が異なっています.これは,基準とする人間によって確率が異なっているということになります.このような主観性を持った確率を「主観確率」といいます.
つまり,このモンティ・ホール問題で考えている「確率」は,あなたが今まで学んできた確率の考え方は通用しないんですね!!!この認識間違いが全ての問題を引き起こしているのです.
かといって,主観確率と客観確率が全く違うもの,というわけではないのが厄介なところです.主観確率は,客観確率と等しくなる場合が多いからです.たとえば,サイコロを振って1が出る確率は,客観確率でも主観確率でも1/6と言えるわけです.言いかえると,これまで勉強してきたところでは主観確率と客観確率が一緒だったので,違いを気にしなくて良かったともいえます.しかし,モンティ・ホール問題では,この二つが異なっています.これが二通りの意見を生み出してしまっているわけですね.
でも,モンティ・ホール問題は,主観確率で考えてください!なんて書いてないじゃん,というあなた.その通りです.これが問題を厄介にしているポイントでもあります.その辺も後々触れていきたいと思います.今回は,確率が二種類あるってことだけ覚えておいてください.
さぁ,次回以降は実際に,主観確率によってモンティホール問題が解かれていく過程を示したいと思います.
それでは〜
次 ⇒ 確率(番外2)モンティ・ホール問題2
今日は最近有名な確率の問題として知られている,モンティ・ホール問題についてです.この問題についての議論をすると,正解は知られているのにそれでも納得のいかない人が現れたりする問題であり,正確な理解にたどり着くのが難しい問題として知られています.
今回はそれを分かりやすく説明していきたいと思いますが,なにぶん難しい問題ではあるんで,誤解を恐れずに自分なりの解釈で説明していきたいと思います.(なので,微妙に間違ってるかも(笑))
さて,それではモンティ・ホール問題とは何か?から行ってみましょう.下に,Wikipediaで示されている問題文を抜粋しています.
「プレイヤー(解答者)の前に3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろにはヤギ(はずれを意味する)がいる。プレイヤーは新車のドアを当てると新車がもらえる。プレイヤーが1つのドアを選択した後、モンティ(司会者)が残りのドアのうちヤギがいるドアを開けてヤギを見せる。
ここでプレイヤーは最初に選んだドアを、残っている開けられていないドアに変更しても良いと言われる。プレイヤーはドアを変更すべきだろうか?
問題のルール:
(1) 3つのドア (A, B, C) に(景品、ヤギ、ヤギ)がランダムに入っている。
(2) プレイヤーはドアを1つ選ぶ。
(3) モンティは残りのドアのうち1つを必ず開ける。
(4) モンティの開けるドアは、必ずヤギの入っているドアである。
(5) モンティはプレーヤーにドアを選びなおしてよいと必ず言う。 」
さぁ,答えはおわかりでしょうか?
ま,いきなり答えを言ってしまいますと,ドアを変更した方が良い,となります.最初に選択したドアに新車がある確率は1/3であり,変更した先のドアにある確率は2/3なんです.
この解答に対し,多くの人が疑問を唱えたのです.どっちも同じ1/2じゃないのか?と言ったわけですね.
あなたはどちらが正しいと思ったでしょうか?
さて,問題をシンプルに考えてみましょう.最初に一つ選んだときに,正解である確率は1/3です.これはいいですね.
その後で,モンティが不正解のドアを一つ開けます.この行動によって,確率が変わっているわけです.つまり,開けることによって消えた1/3の確率分がどこへ行くのか,という話になります.
これが全て,選択していないドアに割り振られたら2/3になります(図の(1)),
残り二つのドアに平等に割り振られれば,1/2になるわけです(図の(2)).
この割り振りが,どういう計算によって導かれるのかについては,次回以降においておきます.ここではその前に,なぜ,二通りの意見が生まれてきてしまうのかを考えたいと思います.その原因はなんなのでしょうか?
じつは,その原因は非常に根本的な部分にあります.
それは,「そもそも,この問題の答えって確率で計算できるの?」という点です.
だって考えてみてください.この問題,司会者であるモンティは正解を知っています.でなければ,不正解のドアを開けることができません.解答者が「このドアが正解である確率は2/3だ!」って言っているよこで,モンティは「いや,そっちは不正解だから.見当違いだねー」と思っているわけです.つまり,司会者からしてみれば,確率の問題ではなく,厳然たる事実なわけです.
これまで説明してきたサイコロの問題では,確率が1/6というのは誰にとっても同じでした.「このサイコロは次に振ったとき,1が出るのさ!」と分かっている人はいないわけです.
なにやら,おかしな感じがしてきていませんか?実はこの不整合さが,問題をややこしくしているんです.
そう,この不整合さはどうして生じているのか,その答えをお教えしましょう.
実は,確率は二種類存在するんです!!!!!
そう.モンティ・ホール問題で問われている「確率」と,今まで学習してきた,サイコロの出る目の確率などの指す「確率」は,似て非なるものなんです.
サイコロの出る目の「確率」などは,誰の目から見ても同じである事実を指しています.このような客観性を持っている確率のことを「客観確率」と言います.
しかし,モンティ・ホール問題の指す確率はそうではありません.司会者と解答者とでは見ている確率が異なっています.これは,基準とする人間によって確率が異なっているということになります.このような主観性を持った確率を「主観確率」といいます.
つまり,このモンティ・ホール問題で考えている「確率」は,あなたが今まで学んできた確率の考え方は通用しないんですね!!!この認識間違いが全ての問題を引き起こしているのです.
かといって,主観確率と客観確率が全く違うもの,というわけではないのが厄介なところです.主観確率は,客観確率と等しくなる場合が多いからです.たとえば,サイコロを振って1が出る確率は,客観確率でも主観確率でも1/6と言えるわけです.言いかえると,これまで勉強してきたところでは主観確率と客観確率が一緒だったので,違いを気にしなくて良かったともいえます.しかし,モンティ・ホール問題では,この二つが異なっています.これが二通りの意見を生み出してしまっているわけですね.
| ◆ 付け足しメモ ◆ 主観確率は,人間それぞれに設定されるものであり,その人間の考え方や信念に依存します.つまり,「誰がなんと言おうと,俺はこの確率は1/4だと思う!」と言えば,その人にとっての主観確率は1/4となります.まーそれでは数学にならないため,数学においては人の考え方や信念は排除し,事実だけから計算できるようにルール設定します. モンティ・ホール問題のルール説明時に,やたらと「必ず〜する」のような表記があるのはそのためです.つまり,「必ず〜するとは限らない」と解答者が思ってしまうようでは,考え方や信念がからんでしまい,数学的に計算できなくなるのです. |
でも,モンティ・ホール問題は,主観確率で考えてください!なんて書いてないじゃん,というあなた.その通りです.これが問題を厄介にしているポイントでもあります.その辺も後々触れていきたいと思います.今回は,確率が二種類あるってことだけ覚えておいてください.
さぁ,次回以降は実際に,主観確率によってモンティホール問題が解かれていく過程を示したいと思います.
それでは〜
このモンティ・ホール問題などで使われている主観確率は,ベイズ確率などとも呼ばれています.このあたりは,ベイズ統計学と呼ばれる分野であり,この理論は現在のIT技術を支えています.たとえばGoogleなどの検索エンジンなどは,この技術なくして生まれていません.しかし,このあたりの理論は様々な前提知識が必要となってきます.
この本では,このあたりの必要な知識を基本から分かりやすく説明してくれている本であり,古典統計学とも呼ばれる,客観確率を基礎とした統計学との違いなども明確に示してくれています.もちろん,このサイトでもある程度説明していく予定ですが,これからさらに重要度を増していく分野であると思いますので一冊ご購入してみてはいかがですか? |
次 ⇒ 確率(番外2)モンティ・ホール問題2
【確率の最新記事】








この記事へのコメント