������₷�����Z���w:�m��(10)���Ғl
�O��@�ˁ@�m��(9):��ʂȂ��̏���
�\��ڂ��[�I�悤�₭�I����C�����T�N�T�N�s�������D�����͊��Ғl�ł��ˁD���wA�Ɋ��Ғl�����������Ƃ�m�����̂����ŋ߂Ƃ����͓̂����ł��D
���Ғl�ň�ԕ�����₷���̂̓M�����u���ł��D���C������Ƃ����M�����u�����l���܂��傤�D�M�����u�������̐l��������Ƃ��t���������������i�j
���āC�T�C�R�������U���āC�����U���o����600�~���炦��M�����u��������Ƃ��܂��D�������C�����U���o�Ȃ������ꍇ�͋t��150�~����Ȃ���Ȃ�܂���D���āC���̃M�����u���C���ׂ����ǂ����H�Ƃ����̂����ł��D�����C���ׂ�����߂�ׂ����D�ǂ��炾�Ǝv���܂����H�������C�M�����u�������������߂�ׂ��C�Ƃ����̂͋p���ł��i�j
���̃M�����u���́C600�~���炦�邩�C150�~�������ƂɂȂ邩�Ƃ�����ʂ�̌��ʂ�������܂����D���Ȃ����M�����u�����������ɁC���̂ǂ���ɂȂ邩�͌��ǐ_�݂̂��m��ł��D������_�ɕ����Ă��������D�ȏ�I�I�I�I�E�E�E�ł͐��w�ɂȂ�܂���ˁD�ł͂ǂ�������画�f�ł���ł��傤���H
���̏ꍇ�C��������l�������Ȃ��������Ȃ��Ă��܂��܂��D�^����ŁC��ʂ�̌��ʂɂ����Ȃ�Ȃ��ł�����ˁD�����ł����������P���l����Ƃ�����C�S�����M�����u��������Ƃ��̌��ʂ����킹�čl����C���̃M�����u�������Ȃ̂����Ȃ̂����͂����肵�Ă��܂����D
�������C�����͈�l�������܂���D���̏ꍇ�ǂ��l���邩�I�����C���������Ă��܂������̂ł����I�I�I�I�I
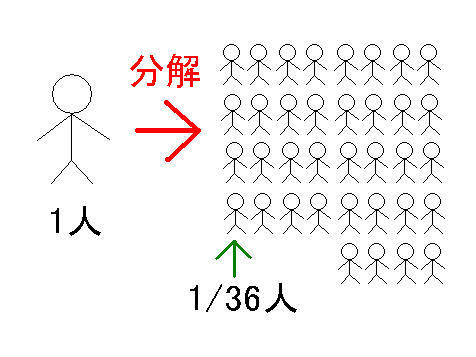
��������������̎����ւƕ������āC���ꂼ��ɃM�����u������点�Ă������Ƃ��́C���̌��ʂ��W�v����Ηǂ��̂ł��I�I���āC���ۂɂ���Ă݂܂��傤�D
��������̎������������ɁC�M�����u���ɏ������ƁC�M�����u���ɕ����鎩�����ǂ̂��炢����̂����܂��l���܂��D�T�C�R���łU���o��Ώ����Ȃ킯�ł�����C���̊m����1/6�ł��D�t�ɕ�����m���C�U�ȊO���o��m����5/6�ł��D�܂��l�̎��������ăM�����u������点����C1/6�l�̓M�����u���ɏ����C5/6�l�̓M�����u���ɕ����邱�ƂɂȂ�܂��D�i�����̐l�����C��������m���Ɠ����ł���_�ɒ��ӂ��Ă��������ˁj
���āC�M�����u���ɏ��Ă�600�~���炦��킯�ł�����C�M�����u���ŏ��������z��
�@600�~×1/6�l��100�~�@�ł��D
����C�M�����u���ɕ������ꍇ150�~�����킯�ł�����C�M�����u���ɕ��������z��
�@150�~×5/6�l��125�~�@�ł��D
����āC�S���i�Ƃ����Ă�������l���ł����j�̃M�����u�����ʂ̑��z�́C
100�~�i6���o���ꍇ�j - 125�~�i6�ȊO���o���ꍇ) �� -25�~

�����Ă�[�I�I�I�����Ă�[�[�[�I�I�܂�C���̃M�����u�������ƁC25�~������Ƃ������Ƃł��D�������͂����܂ŁC�����̎������M�����u�����s�������̕��ϓI�Ȓl�ł��D���ۂɂP��M�����u����������C600�~���炦�邩�C150�~�������̂ǂ��炩��������܂���D�����C���̃M�����u���������₷���Ƃ������Ƃ͕�����킯�ł��D
����-25�~�Ƃ����l�̂��Ƃ��C���Ғl�ƌ����܂��D�܂�C���̃M�����u���ŕ��ϓI�ɓ����錋�ʂ̂��Ƃ��w���܂��D
���āC���Ғl�̈�ʓI�Ȍv�Z���@�ɂ��Đ������܂��傤�D��{�I�ɂ͐�قǎ������悤�ɁC
���̌��ʂœ�����l�@×�@�������������̐l��
���C�S�����������킹�邱�ƂŁC���Ғl�͓����܂��D�����ŁC��������l���Ƃ���ƁC��قǂ̘b�̒��Ŏ������悤�ɁC�������������̐l���́C���̎��ۂ̔����m���Ɠ����ł��D����āC��̎������ۂ��g���ď���������ƁC
���̎��ۂœ�����l�i�M�����u���̌��ʂ̋��z�j�@×�@���̎��ۂ̔����m���i���̃M�����u�����ʂɂȂ��Ă��܂����l���j
������C�S���ۑ������킹�����̂Ɠ����ł��D
���āC����ɂĐ��w�`�̊m���ɂ������{�����̐����͏I���ł��D�����ƍׂ����b�͐F�X����킯�ł����C�}���Ă����ׂ��d�v�ȓ_������������Ă��܂��D���̂��Ƃ́C���̍l�����̗��p�ł����Ă��Ȃ�Ƃ��Ȃ�܂��D�ׂ�������������������قǁC���w���ĕ�����ɂ����Ȃ�悤�Ɏv����ł���ˁD�ق�Ƃɏd�v�ȓ_������������C���Ƃׂ̍������Ƃ��������₷���Ȃ邵�C�Ƃ����₷���Ȃ�̂ł́C�Ǝv���ď����Ă��܂��D
���āC���̌㉽�́C���ۂ̖��ɑ��Ăǂ��l���Ă������������C�������̕����������Đ������Ă��������Ǝv���܂��D�i�������C�����ƍׂ��������Ȃǂ�m�肽���ꍇ�́C�ق��̃T�C�g�ׂĂ݂�̂��ǂ��Ǝv���܂��D�����Ŏ������b��}���Ă����C�������₷���Ȃ��Ă���̂ł͂Ɗ��҂��Ă��܂��i�j�j
��[�ł��C���̑O�Ɋb�x������������ȁ[�Ƃ��v���Ă��܂��D���b�Ƃ��ď��������ȁ`�Ǝv���Ă��邱�Ƃ�����̂ŁE�E�E�܁C���̂ւ�͂��������D
����ł́[�D
���@�m��(11)���ۂ̖��ɑ���(�O��)
�\��ڂ��[�I�悤�₭�I����C�����T�N�T�N�s�������D�����͊��Ғl�ł��ˁD���wA�Ɋ��Ғl�����������Ƃ�m�����̂����ŋ߂Ƃ����͓̂����ł��D
���Ғl�ň�ԕ�����₷���̂̓M�����u���ł��D���C������Ƃ����M�����u�����l���܂��傤�D�M�����u�������̐l��������Ƃ��t���������������i�j
���āC�T�C�R�������U���āC�����U���o����600�~���炦��M�����u��������Ƃ��܂��D�������C�����U���o�Ȃ������ꍇ�͋t��150�~����Ȃ���Ȃ�܂���D���āC���̃M�����u���C���ׂ����ǂ����H�Ƃ����̂����ł��D�����C���ׂ�����߂�ׂ����D�ǂ��炾�Ǝv���܂����H�������C�M�����u�������������߂�ׂ��C�Ƃ����̂͋p���ł��i�j
���̃M�����u���́C600�~���炦�邩�C150�~�������ƂɂȂ邩�Ƃ�����ʂ�̌��ʂ�������܂����D���Ȃ����M�����u�����������ɁC���̂ǂ���ɂȂ邩�͌��ǐ_�݂̂��m��ł��D������_�ɕ����Ă��������D�ȏ�I�I�I�I�E�E�E�ł͐��w�ɂȂ�܂���ˁD�ł͂ǂ�������画�f�ł���ł��傤���H
���̏ꍇ�C��������l�������Ȃ��������Ȃ��Ă��܂��܂��D�^����ŁC��ʂ�̌��ʂɂ����Ȃ�Ȃ��ł�����ˁD�����ł����������P���l����Ƃ�����C�S�����M�����u��������Ƃ��̌��ʂ����킹�čl����C���̃M�����u�������Ȃ̂����Ȃ̂����͂����肵�Ă��܂����D
�������C�����͈�l�������܂���D���̏ꍇ�ǂ��l���邩�I�����C���������Ă��܂������̂ł����I�I�I�I�I
��������������̎����ւƕ������āC���ꂼ��ɃM�����u������点�Ă������Ƃ��́C���̌��ʂ��W�v����Ηǂ��̂ł��I�I���āC���ۂɂ���Ă݂܂��傤�D
��������̎������������ɁC�M�����u���ɏ������ƁC�M�����u���ɕ����鎩�����ǂ̂��炢����̂����܂��l���܂��D�T�C�R���łU���o��Ώ����Ȃ킯�ł�����C���̊m����1/6�ł��D�t�ɕ�����m���C�U�ȊO���o��m����5/6�ł��D�܂��l�̎��������ăM�����u������点����C1/6�l�̓M�����u���ɏ����C5/6�l�̓M�����u���ɕ����邱�ƂɂȂ�܂��D�i�����̐l�����C��������m���Ɠ����ł���_�ɒ��ӂ��Ă��������ˁj
���āC�M�����u���ɏ��Ă�600�~���炦��킯�ł�����C�M�����u���ŏ��������z��
�@600�~×1/6�l��100�~�@�ł��D
����C�M�����u���ɕ������ꍇ150�~�����킯�ł�����C�M�����u���ɕ��������z��
�@150�~×5/6�l��125�~�@�ł��D
����āC�S���i�Ƃ����Ă�������l���ł����j�̃M�����u�����ʂ̑��z�́C
100�~�i6���o���ꍇ�j - 125�~�i6�ȊO���o���ꍇ) �� -25�~
�����Ă�[�I�I�I�����Ă�[�[�[�I�I�܂�C���̃M�����u�������ƁC25�~������Ƃ������Ƃł��D�������͂����܂ŁC�����̎������M�����u�����s�������̕��ϓI�Ȓl�ł��D���ۂɂP��M�����u����������C600�~���炦�邩�C150�~�������̂ǂ��炩��������܂���D�����C���̃M�����u���������₷���Ƃ������Ƃ͕�����킯�ł��D
����-25�~�Ƃ����l�̂��Ƃ��C���Ғl�ƌ����܂��D�܂�C���̃M�����u���ŕ��ϓI�ɓ����錋�ʂ̂��Ƃ��w���܂��D
���āC���Ғl�̈�ʓI�Ȍv�Z���@�ɂ��Đ������܂��傤�D��{�I�ɂ͐�قǎ������悤�ɁC
���̌��ʂœ�����l�@×�@�������������̐l��
���C�S�����������킹�邱�ƂŁC���Ғl�͓����܂��D�����ŁC��������l���Ƃ���ƁC��قǂ̘b�̒��Ŏ������悤�ɁC�������������̐l���́C���̎��ۂ̔����m���Ɠ����ł��D����āC��̎������ۂ��g���ď���������ƁC
���̎��ۂœ�����l�i�M�����u���̌��ʂ̋��z�j�@×�@���̎��ۂ̔����m���i���̃M�����u�����ʂɂȂ��Ă��܂����l���j
������C�S���ۑ������킹�����̂Ɠ����ł��D
| �� �t���������� �� ���Ȃ݂ɂ����Ă��̃M�����u���͊��Ғl���}�C�i�X�C�܂葹����v�Z�ɂȂ��Ă��܂��D���Ȃǂ�300�~�����ē�������z�̊��Ғl��150�~���x�ł��D�܂蔃�����Ƃɔ��z�����킯�ł��ˁD�������^���悯��R���~��ɓ��邱�Ƃ�����̂ł����C���Ȃ������ϓI�ȉ^�̎�����ł���C���z��������Ƃ������ƂɂȂ�킯�ł��D |
���āC����ɂĐ��w�`�̊m���ɂ������{�����̐����͏I���ł��D�����ƍׂ����b�͐F�X����킯�ł����C�}���Ă����ׂ��d�v�ȓ_������������Ă��܂��D���̂��Ƃ́C���̍l�����̗��p�ł����Ă��Ȃ�Ƃ��Ȃ�܂��D�ׂ�������������������قǁC���w���ĕ�����ɂ����Ȃ�悤�Ɏv����ł���ˁD�ق�Ƃɏd�v�ȓ_������������C���Ƃׂ̍������Ƃ��������₷���Ȃ邵�C�Ƃ����₷���Ȃ�̂ł́C�Ǝv���ď����Ă��܂��D
���āC���̌㉽�́C���ۂ̖��ɑ��Ăǂ��l���Ă������������C�������̕����������Đ������Ă��������Ǝv���܂��D�i�������C�����ƍׂ��������Ȃǂ�m�肽���ꍇ�́C�ق��̃T�C�g�ׂĂ݂�̂��ǂ��Ǝv���܂��D�����Ŏ������b��}���Ă����C�������₷���Ȃ��Ă���̂ł͂Ɗ��҂��Ă��܂��i�j�j
��[�ł��C���̑O�Ɋb�x������������ȁ[�Ƃ��v���Ă��܂��D���b�Ƃ��ď��������ȁ`�Ǝv���Ă��邱�Ƃ�����̂ŁE�E�E�܁C���̂ւ�͂��������D
����ł́[�D
���w�K�[������`���Ă����Ȃ���C�������Ă��Ȃ������̂ʼn��ɒu���Ă����܂��D�t�B�{�i�b�`����Ƃ��C���i�̐����Ŏg��Ȃ���ˁ[�Ƃ����悤�Ȃ��b�ł��C�����������`�Ō�������Ƌ����������Ă�����̂��ȁ`�ƁD���w�̖ʔ����ɐG���ɂ͗ǂ��Ǝv���܂��D
����ŃT�N�T�N��߂āC���w�ɂ����������Ă�Ȃ�C���ꂪ��Ԃł���ˁ`�D�����Ɛ��������̕��͓͂ǂ݂ɂ����ł���C���ہD���w�D���Ȑl�́C�����Ȃ炢����ł��ǂ߂���Ă�����ł����ǁC���������ł��Ȃ�������i�j |
���@�m��(11)���ۂ̖��ɑ���(�O��)
�y�m���̍ŐV�L���z












