【Excelショートカット豆知識】
[Ctrl]+ ] そのセルが参照しているセルへジャンプ
[Ctrl]+ [ そのセルを参照しているセルへジャンプ
新しい座標系は元の座標に対して鏡面対称となっています
任意の点を x 軸に関して対称移動させる操作は線型変換の代表的な例といえます:

たとえば三角形をこの行列で変換すると、下図のようになります:
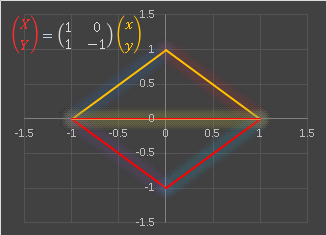
黄色の三角形が x 軸に対して折り返されて赤い三角形に移っています。これは x-y 座標での変換の様子ですね。前回お話した座標変換の考え方を練習してみます。ベクトル (1, 1) を変換した様子を図示すると・・・・・・
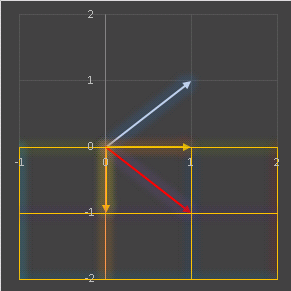
水色のベクトル (1, 1) が赤いベクトル (1, -1) に変換されています。これは、ベクトル (0, 1) と ベクトル (0, -1) という2つのベクトル(基底)を格子とする座標に移されたと考えることができます。この新しい座標系における赤色のベクトルは、やはり (1, 1) と表されることになります。今の場合は
新しい座標系は元の座標に対して鏡面対称となっている わけです。
2 行 2 列で十分です
「座標変換」とか「線型結合」なんて言われると思わず身構えてしまいそうですが、丁寧に咀嚼して頭を慣らしていくと、別にどうということはありません。前回も言いましたが、紙と鉛筆を用意して何度か練習していれば、すぐにコツを掴めます。扱う行列はとりあえず 2 行 2 列で十分です。多くても 3 行 3 列までにしておいたほうがいいです。次元が大きくなると書くのが面倒になってくるし、計算間違いをしやすくなるからです。特に行列式の計算なんかで次元が大きいと「うぎー!」となります。大学で使う線型代数学の教科書には1つ1つの定理の証明に m 行 n 列に一般化した行列が用いられていますが、そこも 2 行 2 列、あるいは 3 行 3 列に置き換えてしまったほうがわかりやすいです。 2 行 2 列・ 3 行 3 列でしっかり理解しておけば、あとで自然と m 行 n 列に拡大して考えることができるようになりますし、 m 行 n 列の証明なんて無視してしまっても、たぶん本質の理解の妨げにはならないと思います。こんなこと言うと、数学科の人に怒られるかもしれませんけどね・・・・・・。

