Excel VBA　数学実験室

　今回は改めて 線型変換（１次変換）の意味 を考えてみようと思います。理数系の学生さんは行列の計算をたくさん練習されると思いますが、行列はただ計算規則を定めたものではありません。そこにはちゃんと意味があります。

線型変換（基底とは新しい座標系の単位格子ベクトルです）

　たとえば次のような対角成分の等しい行列による変換を考えてみましょう。

　これを少し変形すると


　のような形にできますね。ベクトル a = (3, 1) と b = (1, 3) による線型結合の形になっています。 (x, y) は任意の点ですから、「 x-y座標上のあらゆる点が a と b の線型結合の上に乗りますよ」ということです。つまり (X, Y) は a と b によって作られる格子で表される新しい座標ということになります。任意の点ではわかりにくいかもしれませんので、(1, 1) と (2, 2) を試しに変換してみます：


　これを図示すると下のようになります。

　　

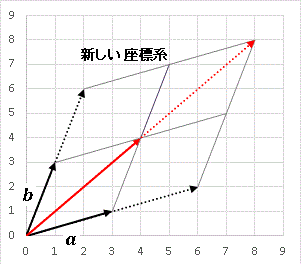
　(1, 1), (2, 2) はそれぞれ x-y 座標系では (4, 4), (8, 8) に移っているわけですが、X-Y 座標ではやはり (1, 1), (2, 2) と表されます。ただし、その格子単位は a と b の長さになっているのです。このように解釈すると、 2 行 2 列の行列は 2 次元ベクトルを２つ横に並べたものと考えることができます。そしてこの２つのベクトルを基底とよびます（つまり 新しい座標系の単位格子ベクトル です）。
　以上のことを踏まえると、行列計算にある程度習熟したら（これはとても大切なことで無意識にできるようにならないといけません）、少し面倒かもしれませんが、行列をベクトルに分解し、実際に紙にベクトルで作った格子を書いてみて、「どういうふうに変換されたのかな？」と確認することを繰り返してみてください。適当な行列を選んで１０回ぐらいやってみると、線型変換の本質が必ず「見えて」きます。

　これまで何度も取り扱ってきた回転行列による線型変換を「線型結合」の視点で見直してみます。回転行列 R_θ による変換を次のように書き表します：


　ベクトル a = (cosθ, sinθ) は円周上の点ですね。



ですから、ベクトル b = (- sinθ, cosθ) もやはり円周上の点で、 a を反時計回りに 90°回転させたベクトルです。 a と b の内積をとってみると、


となり直交していることがわかります。また、


もすぐに計算できます。つまり、回転行列 R_θ は座標を反時計回りに回転させ、格子の長さと角度は不変に保ちます。たとえば回転行列で単位ベクトル (1, 1) を変換すると下図のようになります：

　

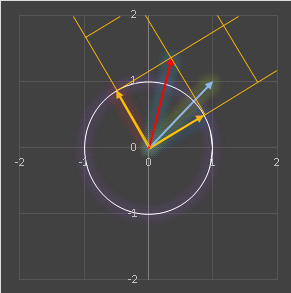
　水色の単位ベクトル e は変換によって a + b と表されますから（赤色ベクトル）、回転した直交座標で (1, 1) と表されます。しつこいようですが、ベクトル (j, k) を線型変換したとき、元の x-y 座標系ではその座標を変えてしまいますが、新しい座標ではそのまま (j, k) となります。
　

サイトをデザインしてみたいです

　今こうして無料ブログ（ファンブログ）を使っているわけですが、いつかは自分でサイトをデザインしたいなと考えています。でもやはり、なかなか時間がとれないですね。Web サイトは CSS と HTML で組み立てるのですが、１から作ろうと思うとまるまる１週間ぐらいの作業量を必要とします。なので「明日からやろう」ということがずっと続いて今に至り、全く手をつけられない状況が続いています・・・・・・。

イメージを掴みましょう

　理工系の人が大学に進学してすぐに学ぶのが「線型代数学」です（文系の人も教養学部で選択することがあるかもしれません）。理工系の様々な分野で「線型代数学」は使われています。線型変換（１次変換）、行列式の計算、固有値・対角化などが有名ですね。線型代数学の計算法はコンピューターでは大変使い勝手が良く、実のところ、「線型代数学のなんたるか」なんてことをほとんど知らなくても、けっこう使えちゃったりします。数学を専攻されている人はそんな状況を嘆いて「そんなことじゃ、いかーん！」と叫びたくなるかもしれませんね。でも確かに線型代数学は「ただ使っている」だけでは勿体ないと思うほど、数学的に大事なエッセンスがつまっています。その抽象的なイメージを掴むには少し時間を割かなければいけませんが、早い段階で理解を深めておけば、その時間は決して無駄にはならないと思います。