ベッセル回転行列による円の変換
行列 Bθ の定義を再掲します:右下の添え字θは回転角を表すと決めておきます。前回はこの行列による繰返し変換によって点の軌跡を追いましたが、今回は普通に円に対して行列を作用させて、その変形を見ます。 B0 による変換は:

円に対して不動となります。B60 で試してみましょう:
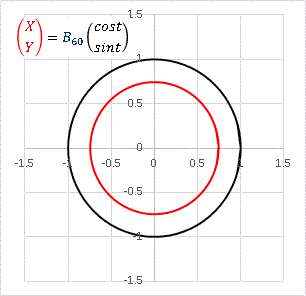
円を縮小させました。ベッセル関数のもつ振幅減衰効果が図形に対する1次変換ではこのように表現されるわけです。点に対する繰り返し変換の軌跡は螺旋でしたね。 B180 で試してみると:
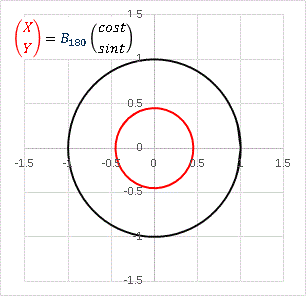
もっと小さくなりました。θ → ∞ の極限で円は点に圧縮されます。しかし、これだけではベッセル回転行列の面白さは理解できません。単に図形を縮小(或いは拡大)させるだけなら普通の対角行列で表現できます。
ベッセル回転行列による二等辺三角形の変換
ベッセル回転行列は円以外の別の図形に作用させてはじめて、その奇妙な性質が見えてきます。たとえば、この行列で (1,0), (-1,0), (0,1) を頂点とする二等辺三角形を変換してみると、θ の値によって次のように変化します。
三角形を反時計周りに回転させつつ縮小させる行列であることがわかりますね。θの値を大きくとるほど変換される三角形は小さくなります:
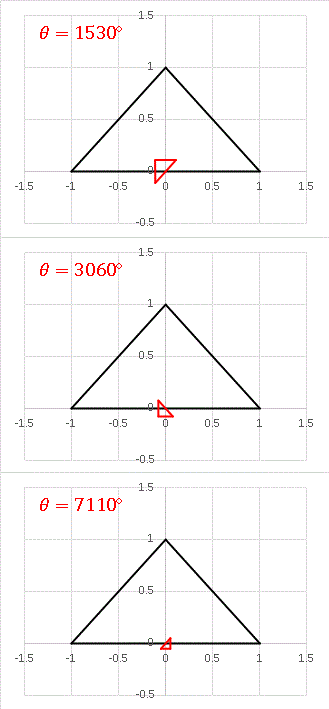
米粒のように小さくなってしまいましたね。 θ → ∞ の極限で三角形の面積は 0 になります。
アメショを飼ってます
英語ノートで綴っている「こばとちゃん」シリーズの小春ちゃんも猫を飼っている設定にしてあります。種類は私の飼い猫と同じアメリカンショートヘアーですが、性別は男の子にしておきました。私の飼い猫が女の子なので、アメショの男の子がどういう性格なのかは詳しく知らないのですが(猫は性別によって性格がまるで違います!)、猫雑誌などをみると「大らか」、「細かいことを気にしない」というようなことを書いてあるので、小春ちゃんの飼っている「うななん子たん」もそういうざっくばらんな性格にしておきました。私の飼い猫の性格は真逆で、とにかく真面目で、しっかりものです。立ち姿もぴしっとしています。私も見習いたいと思うぐらいです。やっぱり猫が好き
猫が大好きなので、自宅は猫グッズだらけです。猫の雑誌、猫の置物、猫カレンダー・・・・・・。携帯の待受けも当然にゃんこです。自分でも「うーむ。ちょっとおかしいかもしれないな」と思ったりもするのですが、猫が好きなので仕方ありません。そんな猫好きを知ってくれている友人は猫マグカップをくれました。これは猫ちゃんが立って両手を伸ばしている絵が書かれていて、今までみたことないほど、本当にセンスのあるカップなのです。これは数ある猫グッズの中でも、いちばん大切な品物です。「これだけは絶対に割ってはいけない!」と思い、洗う時は他の食器とは別にして、慎重に丁寧に扱っています。