Excel VBA　数学実験室

　今回はベッセル関数を使用します。
　整数次ベッセル関数を再掲しておきます。




　ベッセル関数は三角関数によく似た周期関数ですが、 x の増加と共に（1 / √x に比例して）振幅を減衰させていきます。

内側の楕円と外側の楕円を行ったり来たりするグラフ

　三角関数を用いて

　　　　x = a cosθ ,　y = a sinθ

　という媒介変数で関数を定義すると、半径 a の円を描くことはよく知られていますね。これと同じようなことをベッセル関数を用いて試みます。媒介変数θの範囲は -4pi < θ < 4pi とし、番号 n は 0, 1 を選択します。つまり、

　　　　x = J₀(θ) ,　y = J₁(θ)

によって (x, y) を定義し、グラフを描いてみます：

　

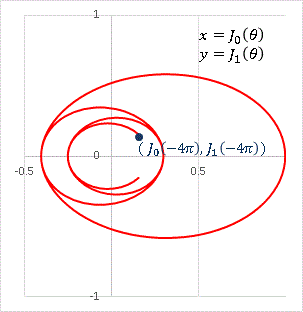
　楕円の内側に楕円が入っています。θの範囲を広げれば、内側の楕円の数はどんどん増えていきます。青い点で示してあるのがスタート地点の (J ₀(-4pi), y = J ₁(-4pi)) で、θの増加と共に順次外側の楕円へ出て行き、１周するとまた内側の楕円へ戻っていきます。ちょっと疲れますけど、眼で追って行けば軌道がわかります。
　上の組合せは楕円を描きましたが、 n の選択の仕方によってはまた異なる軌道が描かれます。n = 3, 5 を選択してみましょう。すなわち、

　　　　x = J₃(θ) ,　y = J₅(θ)

で関数を定義してグラフを描きます：

　

　最初は内側から楕円のような軌道を描きますが、次第に崩れて外側で大きな８の字軌道を描き、再び内側の軌道へ戻って来ます。
　　

線形代数学を予定しています

　そろそろ線形代数学を取り扱ってみようと考えています。中でも特にお馴染みの行列による１次変換ですね。１次変換のように、ある図形を別の図形に変換するという作業を紙と鉛筆で勉強するには（或いは実感するには）どうしても限界があります。限られた時間の中で変数をちゃかちゃか変えながら、どういう種類の行列なのかを確認するためにはコンピューターの力を借りる必要があります。次の次ぐらいに、まずは有名な回転行列とその変形版を取り上げてみる予定です。お楽しみに。