圧縮される波形
今回は y = sin(xsinx) という関数のグラフを描いてみます。
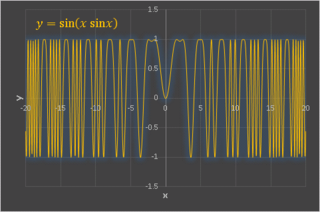
原点から遠ざかるにつれて波が 圧縮 されています。
sin の中身を xcosx に変えてみましょう。
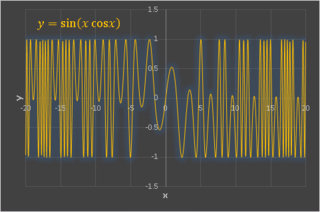
これは原点対称の関数です。
やはり原点から遠いところでは 波長が短く なります。
y = sin(xlogx2)
次は y = sin(xlogx2) という関数です。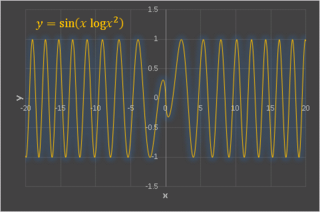
緩やかにではありますが、やはり原点から遠ざかるにしたがって波長は短くなっていきます。
伸張と圧縮
最後は y = sin(xsin(logx2)) という関数です。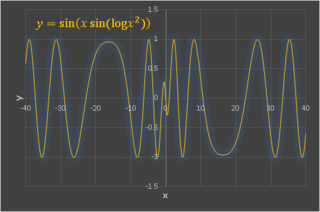
この関数で表される波は複雑な振る舞いをします。
x = ±20 のあたりまでは波長が広がり、それより遠いところでは逆に波長が短くなっていきます。