階乗の対数を計算します
n! の自然対数をとって
f(n) = log(n!)
という数列をプロットしてみます( n ≧ 1 で定義します)。

n! はとても大きな値を返す演算です。たとえば n = 40 であっても
40! = 8.16 × 1047
という巨大数になってしまいます。logx は抑え込みの強い関数なので log(n!) の増加曲線は比較的緩やかになりますが、それでもその増加率は少しずつ大きくなり、たとえば区間 [10, 20] では ⊿f/⊿n ≒ 1.8 であるのに対し、[100, 110] では ⊿f/⊿n ≒ 3.7 に上昇します。そこで log(n!) を n で割ってみると ......
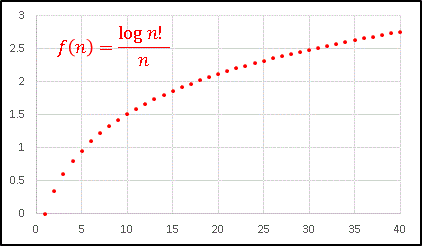
⊿f/⊿n は n の増加と共に小さくなります。
それでもなお n! の寄与が勝って上昇曲線を描いていますね。
log(n!) を n2 で割って初めて減少関数となります。
