ロピタルの定理(簡易版)
-π < x < 0, 0 < x < π の範囲で次のような関数を定義します。この関数のグラフを Excel で描くと次のようになります。
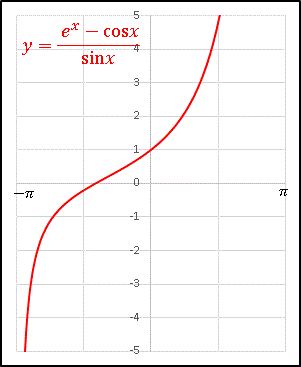
どこにも切れ目のないグラフに見えますね。しかし、もちろん x = 0 では定義されない(分母が 0 になる)関数です。しかし x → ±0 での極限は存在するようです。このような 0/0 型不定形の極限を求めるときに威力を発揮するのが ロピタルの定理(簡易版) です。
[ロピタルの定理(簡易版)] f(x) と g(x) がある開区間で無限回微分可能で、a がこの区間に含まれているとします。そして
=g(a)=0,\quad g'(a) \neq 0)
であるとき、
}{g(a)}=\lim_{x\rightarrow a}\frac{f'(a)}{g'(a)})
が成り立ちます。
であるとき、
が成り立ちます。
実を言うと、本物のロピタルの定理よりも強い仮定を用いています。本物のロピタルの定理は前提条件が大変面倒なので、とりあえず上の条件に当てはまる場合にだけ使うようにしてください。今回扱う関数は分子・分母ともに何度でも微分可能です。
とおくと、
ですから、ロピタルの定理が使えて、
となって、グラフに描かれている通りの極限値を得ることが出来ました。
cosx を乗じます
上の関数に cosx をかけて、x → ±0 で cosx → 1 ですから、先ほどの結果と合わせると、この関数も x → ±0 で極限値 1 をもちます。実際にグラフで確認してみましょう。

点 (0, 1) でつながっているようなグラフになっていますね。もちろん実際には x = 0 で不連続なのですが、この点だけ改めて y = 1 というように定めてやると、連続な関数となります。