[Shift] + ↑ 選択セルを追加しながら上に移動
[Shift] + ↓ 選択セルを追加しながら下に移動
[Shift] + → 選択セルを追加しながら右に移動
[Shift] + ← 選択セルを追加しながら左に移動
円の伸開線(インボリュート)
今回扱うのは 円の伸開線(インボリュート)です。円に巻かれた糸をピンと張りながら解いていくときにできる糸の端点が描く軌跡です。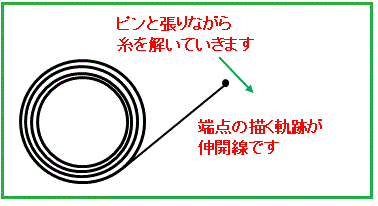
(x, y) は θ を介して次の方程式を満たします。
x = a(cosθ + θsinθ)
y = a(sinθ − θcosθ)
y = a(sinθ − θcosθ)
a = 1 としてグラフを描いてみます:

原点付近から始まって間隔一定の螺旋を描いていますね。伸開線の方程式を次のように変形してみます。
x = a(cosθ + logθsinθ)
y = a(sinθ − logθcosθ)
y = a(sinθ − logθcosθ)
ただし 0 < θ としておきます。 a = 1 のグラフは・・・・・・
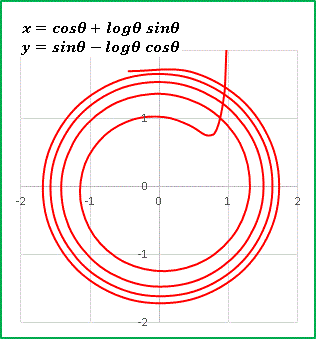
無限遠方からやってきて、(1, 1) 付近をかすめて屈曲します。そのあとは伸開線と同じように螺旋を描き始めますが、間隔は一定ではなく少しずつ狭まっていきます。これはもちろん logθ の影響です。θ が大きくなるほど θ の増加を抑えようとする効果が大きくなるわけです。
伸開線の方程式において、次のように三角関数をベッセル関数に置き換えてみます:
cosθ ⇒ J3(θ)
sinθ ⇒ J0(θ)
方程式は
x = J3(θ) + θJ0(θ)
y = J0(θ) - θJ3(θ)
y = J0(θ) - θJ3(θ)
となります。
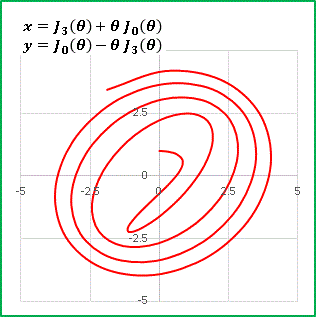
少し傾いた楕円になってはいますが、伸開線とよく似ていますね。最後は sinθ の部分だけを J0(θ) で置き換えた方程式です:
x = cosθ + θJ0(θ)
y = J0(θ) - θcosθ
縦軸・横軸のスケールを揃えたグラフを載せてみましょう:y = J0(θ) - θcosθ
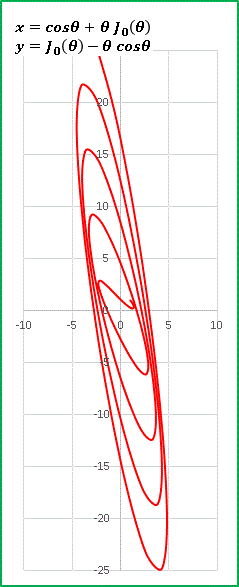
y 軸方向に細長い楕円型螺旋が現れました。