r = f(��)
�̌`�ɕ\���ꂽ���������ɕ������Ƃ�т܂��B�㎮���� (x, y) ���W�́A
x = f(��) cos��,�@y = f(��) sin��
�Ōv�Z����܂��B
���t�Ȑ��i�o���Ȑ��j
�@����͐��t�Ȑ�
r = sin(n��)
�������܂��B����܂ł��T�C�N���C�h��A�X�e���C�h�Ȃǂ��Љ�܂������A���t�Ȑ��͓��a�ƕΊp�̊Ԃ̊W�������ȒP�Ȍ`�����Ă��܂��B�������A���̕������̕`���}�`�̓T�C�N���C�h�E�A�X�e���C�h�������G�Ȍ`�����Ă��܂��B�܂� n �� 1 �̏ꍇ���猩�Ă݂܂��傤�F
�@
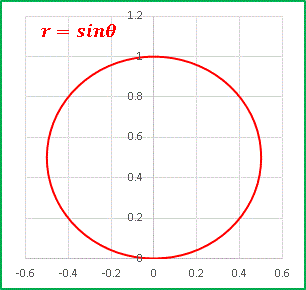
�@����͒��S�_�� (0, 1/2) �Ŕ��a 1/2 �̉~�ł��B n = 2 �Ƃ��Ă݂�ƁE�E�E�E�E�E
�@
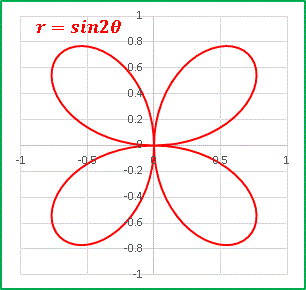
�@�S�̗t������܂����ˁB n = 3, 4, 5 �Ƃ܂Ƃ߂Č��Ă����܂��傤�F
�@
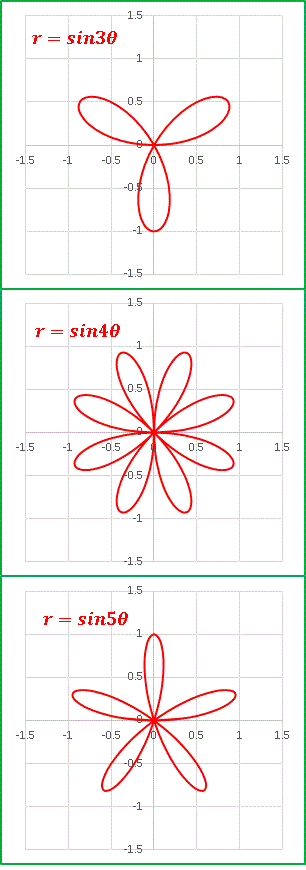
�@n �ɂ���ėt�̐��������܂����An ����������ɉ����ėt��������Ƃ����P���ȊW�ɂ͂Ȃ��Ă��Ȃ��悤�ł��B n = 5 �ł͗t���T���Ɍ����Ă��܂��Ă��܂��ˁB������ n �Ɨt�̐��͔{���W�ɂ���悤�ł��F
n = 1�@�@�t�̐� = 1 = 1n
n = 2�@�@�t�̐� = 4 = 2n
n = 3�@�@�t�̐� = 3 = 1n
n = 4�@�@�t�̐� = 8 = 2n
n = 5�@�@�t�̐� = 5 = 1n
�E�E�E�E�E�E�E�E�E
n = 2�@�@�t�̐� = 4 = 2n
n = 3�@�@�t�̐� = 3 = 1n
n = 4�@�@�t�̐� = 8 = 2n
n = 5�@�@�t�̐� = 5 = 1n
�E�E�E�E�E�E�E�E�E
�@�O���t�͏ȗ����܂����A���l�� n �𑝂₵�Ă����ƁA�t���� 1n, 2n �̐������݂ɂƂ邱�Ƃ��킩��܂��B�������茸������ł��B���āA n = (2m + 1) / 2 �Ƃ����ꍇ�͂�蕡�G�Ȑ}�`��`�����ƂɂȂ�܂��B n = 0.5, 1.5, 2.5 ���܂Ƃ߂Č��Ă݂܂��F
�@
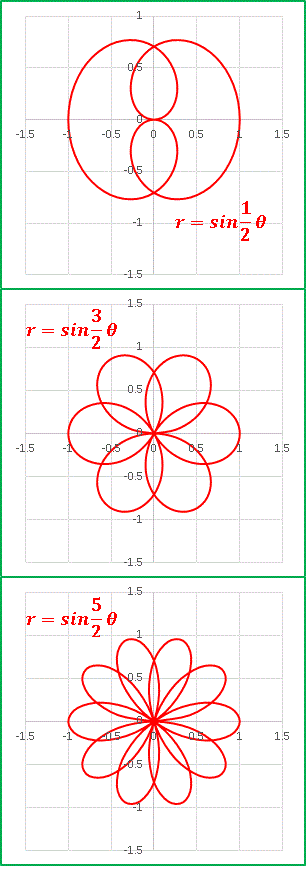
�@���G�ł͂���܂����A�����ȑΏ̐����������������O���t�ł��B�����������ݍ���ł����܂��傤�B n = 0.3 ����� n = 1.3 �͂ǂ��Ȃ邩�E�E�E�E�E�E
�@
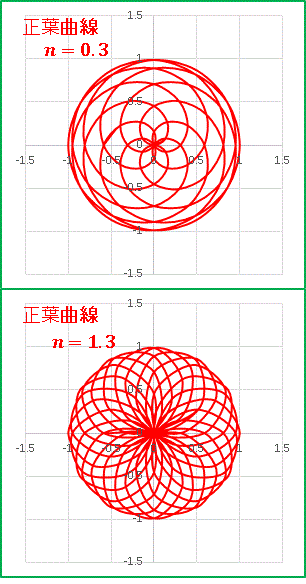
�@���͂�t�̌`�͂��Ă��܂���ˁB�ׂ��ȖԖږ͗l���o���オ���Ă��܂��Bn �������̏ꍇ�Ƃǂ����Ă���ȂɈ���Ă��܂��̂��H�@����͎O�p���̂������Ɍ���������܂��B���Ƃ��A
r = sin[2��]
�Ƃ����������ɂ����ďo���_�i �� = 0 �j�ł�
r = 0
�ł��ˁB���_�ɂ��܂��B�Ƃ����Ă����ƂP�����Ă����ꍇ��
r = sin[2(0 + 2pi)] = sin[4pi] = 0
�Ƃ�͂蓯���l�ɖ߂邱�Ƃ��킩��܂��B�ȍ~�͌J��Ԃ��ł��B�܂� �� ���ǂꂾ���������Ă��A�����Ƃ�����Ȃ��邱�ƂɂȂ�܂��B�Ƃ��낪�A
r = sin[0.3��]
�Ƃ����������̏ꍇ�A�� = 0 �� 2 pi ��������Ɓi�P��������Ɓj�A
r = sin[0.3(0 + 2pi)] = sin[0.6pi]
�ƂȂ�A�P���O�ƕʂ̒l���Ƃ��Ă��܂��܂��B
�@
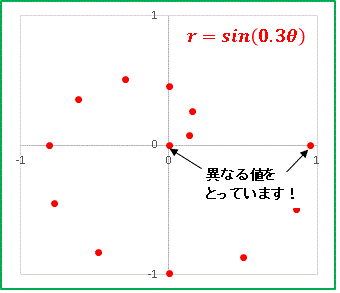
�������炳��� �� �������Ă����ƁA�P���O�Ƃ͕ʂ̓���ʂ邱�ƂɂȂ�A�������Ď��Ƃɏ��������ꂽ�O�Ղ�`�������ĖԖږ͗l�����o���킯�ł��By = sin(nx) �Ƃ����O���t�͂ǂ̂悤�� n ��I�Ƃ��Ă��A�g�`�̎R�ƎR�A�J�ƒJ�̊Ԋu���قȂ邾���ł����A���a r �Ɗ֘A�t����ꂽ�ꍇ�́u�P�����Ƃ̕��ʏ�̈ʒu�̂���v�Ƃ��Č���Ă��܂��B
�@���t�Ȑ��� �� �̌W���ɑ��� sensitive �ɔ������Ă��̗l����ς��܂��B�����Ȃ�A�W���ƎO�p���̎����̑����ɂ���Ă��̌`�����߂܂��B
���t�Ȑ��̕���
�@���t�Ȑ����ǂ����Ă��̂悤�ȓ����I�ȃO���t��`���̂ł��傤�Hr = sin[2��]
�̕��������������������ڂ������ׂĂ݂܂��B���a r �͕Ίp �� �� sin ���ƌ��т��Ă���킯�ł�����A���a�������I�ɐL�k����Ƃ����̂͒����I�ɂ킩��܂��B���� = 15���̎U�z�}�ŗl�q�����Ă݂܂��傤�B���ɓY���Ă���}�� y = sin2x �̃O���t�ł��B
�@
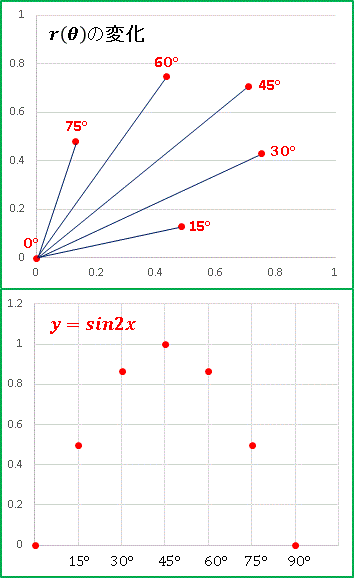
�@sin2x �� 0 ���� 45���܂ő���������ł�����A�����܂ł͗������̂悤�ɓ��a���L�тĂ����܂��B������ 45������ƍ��x�͈�]���ē��a���k�܂��Ă����A�� = 90���Œ����� 0 �ɂ��܂��i���_�ɖ߂�܂��j�B�ł������P�ی��ł͒��� y = x �Ɋւ��đΏ̂ȁu�t�̂悤�Ȍ`�v�̃O���t��`���킯�ł��B
�@
���ƂȂ��̐��w���L
�@�u�p��̊فv�ɓo�ꂷ�鍹���̎��Ƃ͂�����������i�ؕ���j�ł����A�ߏ��̂��X�����f���ɂ��Ă��܂��i�������A���X�̖��O�͕ς��Ă���܂��j�B�����ŐH�ׂ鋼���͂ƂĂ����������ł��B���ʂ��������E�߂ł��B�����A�P�Ɏ����n�R�������炨�E�߂��Ă��邾���ł����A���ɗ]�T�̂���l�͊���Ȃ�V�n�������Ȃ��H�ׂĂ��������B�����Ɣ��������Ǝv���܂��B����A�H�ׂ����ȁE�E�E�E�E�E�B�@ �@