Excel VBA　数学実験室

【エディタのショートカット豆知識】
　[Ctrl] + [Del]　カーソルの位置から行末まで削除する

二つの山に挟まれた窪地のようなグラフ

　双曲線関数（hyperbolic functions）の定義とグラフを紹介します。「知ってるよ！」という人は記事の一番最後のグラフだけ見てください。

　　coshx = [exp(x) + exp(-x)] / 2
　　sinhx = [exp(x) - exp(-x)] / 2
　　sechx = 1 / coshx
　　cosechx = 1 / sinhx

　それぞれ、

　　hypabolic cosine （双曲線余弦）
　　hypabolic sine （双曲線正弦）
　　hypabolic secant （双曲線正割）
　　hypabolic cosecant （双曲線余割）

　と読みます。全てエクセルに予め用意されています。便利な世の中になったものです。しばらくはこれらの関数をベースに色々な関数を組み立ててみます。グラフは次のようになります。




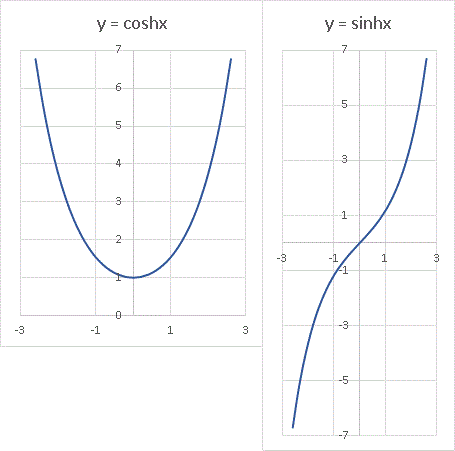
　では sin の中に coshx を入れてみましょう。



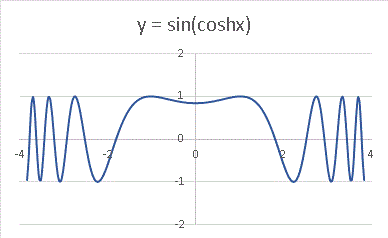
　-1 < x < 1のあたりではのんびりとした関数ですが、そこを超えると激しく振動し、周期は短くなっていきます。x の絶対値が大きくなると、

　　　x < 0 では y ≒ sin[exp(-x)]
　　　0 < x では y ≒ sin[exp(x)]

となるわけです。

　次は y = coshx の肩に sinx をのせます。x の範囲は -2pi≦x≦2pi としておきます。piは円周率です。ブラウザ環境によってはπと n の表示が似ていて紛らわしいので、今後は円周率を pi と表記することにします。



　上のようにやや原点近傍でやや複雑な形のグラフとなります。
　次は y = sin[sech(1/x²)] という関数です。



　式は複雑なのですが、グラフは単純な形をしています。二つの山に挟まれた窪地のような形ですね。

コメントくださいな

　このブログ、まだコメントがありません。どんな人が読んでいるのかわからないので記事の方向性を迷っています。「理学部の学生です」とか「高校生です」などの簡単な一文で構いませんので、コメントをいただけると嬉しいです。また、「こういう関数を扱ってください」というリクエストをいただければ、なるべくお応えしたいと思います。