[Ctrl] + [X] 切り取り
[Ctrl] + [C] コピー
[Ctrl] + [V] ペースト
三角対数と対数関数の積(芸術的な関数?)
三角関数と対数関数の積です。logx が単調増加関数なので、sinx を掛けると x の値と共に振幅が増加するグラフとなります。 0 < x < 1 で logx < 0 であり、その範囲で sinx > 0ですから、両者の積は負になります。x > 1 では logx > 0 ですから関数の正負は sinx の正負と連動します。形を予測することは難しくないですが、手書きで描こうとすると案外面倒です。sinx の部分を sin 2x に代えてみると下のようなグラフになります。

先と同じ理由で 0 < x < 1 で負の値をとりますが、以降は y ≧ 0 です。x = n・pi のときに y = 0 となります(pi は円周率)。

次のグラフは y = logx/(1 + x) という微積分の演習問題によくでてくる関数です。
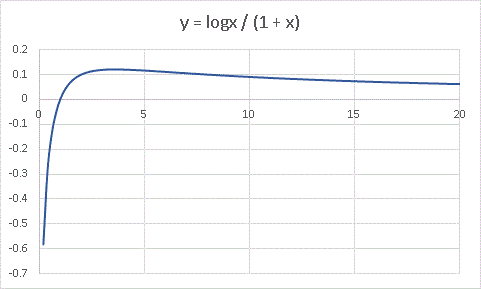
単純に cosx を乗じてみますと・・・・・・
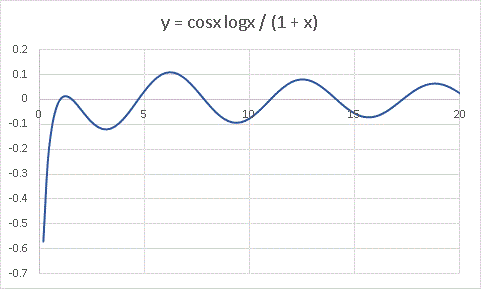
予想通りグラフ全体がぐにゃりと曲がります。では、y = logx/(1 + x) を少し変形して y = log(cosx + 2)/(1 + x) としてみます。log の中身を三角関数に変えてみるのです。中身に 2 を加えてあるのはちょっとしたテクニックです。対数関数は 0 以下の数字をとれないので、普通は変数の絶対値をとって、0 を省くというようなことをやるのですが、cosx は最小でも−1 しかとれないのですから、予め中身に 2 を加えてしまったほうが簡単な式ですみます。ようするに私が楽をできるのです。さて、グラフを描いてみると・・・・・・

地面に落ちたボールがバウンドするような減衰関数であることがわかります。シンプルなグラフではありますが、やはり増減表を作って手書きするのはしんどいと思います。エクセルなら操作に慣れていれば5分で描けます。
上の関数の分子に着目して、
x = log(cosθ + 2)
y = log(sinθ + 2)
という媒介変数表示の関数を作ってみました。

おにぎりみたいな形ですね・・・・・・。これに無理数を変数とした三角関数を加えてみます。

美しい曲線が現れましたね。「おにぎり」から「芸術」に変化しました、とは言い過ぎですかね。
読書が好きです
本を読むのが好きです。ジャンルは純文、歴史、ノンフィクション、ファンタジー、SF ・・・・・・どんな分野でもかまわないという行き当たりばったりな本読みです。古典も好きです。中でも「枕草子」は大和言葉の使い方がとても美しく、一番のお気に入りです。今は語源学にはまっています。英単語のルーツを探っていくと本当に面白いです。アマゾンで海外から本を取り寄せたりしました。それぐらいはまっています。