周期的な結節点 (crunode) をもったグラフを作ります
今回はexp(-x2) + exp(y2) = a [1]
という方程式を扱います。y = f(x) の形で表すと
という多価関数です。ここで平方根の中身が常に正となるように a の範囲を定めておくことにします。すなわち
log [a - exp(-x2)] ≧ 0
となるのは、
a - exp(-x2) ≧ 1
のときです。少し整理すると
a ≧ exp(-x2) + 1
です。exp(-x2) の最大値は 1 なので、
a ≧ 2
と定めておくと、全実数で定義される関数となります。
それでは a = 3.0, 2.5, 2.0 のグラフを描いてみます。
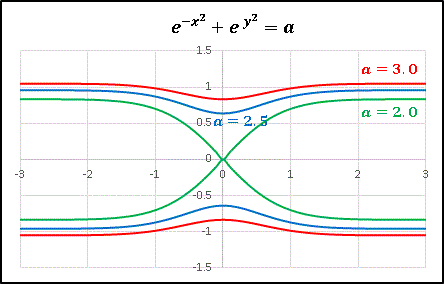
2 価の関数です。 a の値が小さくなるにしたがって、2つの曲線は原点に向けて凹んでゆき、a = 2.0 では原点で交差します。 [2] に三角関数を掛けて
という関数をつくってみると ......
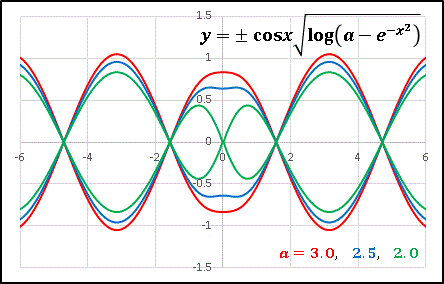
このように 周期的な結節点 (crunode) をもったグラフ になります。