�������ƌ��������
�@�w�����̒��� sinx/x ����ꂽ�����ƒ�`���A����ɐ��������|��������
�ƒ�`���܂��B
�@�@
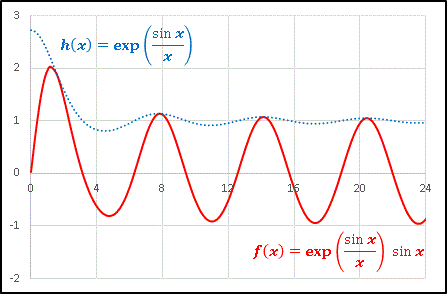
�@�Ԃ������� y = f(x) �A���_���� y = h(x) �ł��B
�@���ϕ��ɂ�����L���ȋɌ��藝
�ɂ���āA
�ƂȂ�܂��B f(x) �̐U���� h(x) �ɉ����Ă�����茸�����܂��B��̐}�ł͂�����ƕ�����ɂ����̂ł����A��������ڂ��Â炷�� h(x) �� f(x) �̋ɑ�l���������� 1 �ɋ߂Â��Ă����܂��B x ���[���ɑ傫���Ƃ���ł� f(x) �� sinx �ƂȂ�܂��B���x�͌��ɂ������Ă��� sinx �� sin(x/2) �ɒu�������āA
�Ƃ��������`���Ă݂܂��B
�@
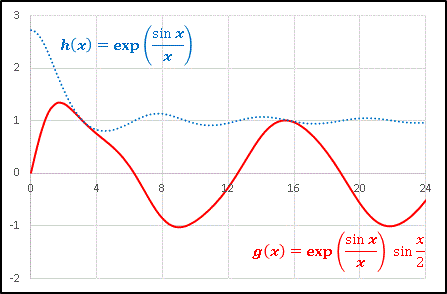
�@x = 4 �̂�����ł��ɂ��ƋȂ����Ă����肵�܂����A�������`�𐮂��āA��͂� x �� �� �ł� g(x) �� sin(x/2) �ƂȂ�܂��B
�@
y = exp(1 / x) �F �}�������
�@����� y = exp(1 / x) �Ƃ��������x�[�X�ɂ��܂��F�@
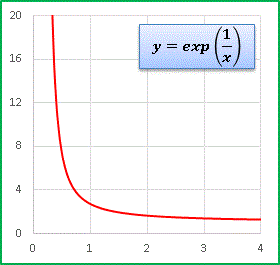
�@[0, 1] �̂�����ŋ}���ɒl�𗎂Ƃ����ł��B
�@���̊��� x 2 ���|���Ă݂܂��F
�@
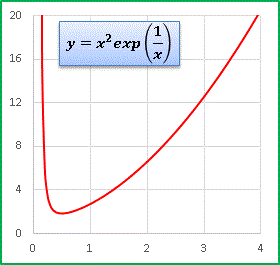
�@�ɏ��l�܂łЂƑ��ɋ}�����āA���̂��Ƃ͑����ɓ]���܂��B
�@���̊����������ƁA
y��= (2x �| 1)exp(1 / x)
x < 1 / 2 �� y�� < 0
x > 1 / 2 �� y�� > 0
x < 1 / 2 �� y�� < 0
x > 1 / 2 �� y�� > 0
�ƂȂ�̂ŋɏ��l�� x = 0.5 �ł��B�A�����ł͂���܂����A���̋ɒl�����ɂ��Ċ��̗l���͈�ς��Ă��܂��ˁBx ���\���ɑ傫���Ƃ���ł� exp(1 / x) �� 1 �Ƃ݂Ȃ���̂ŁA y �� x 2 �ƂȂ�܂��B
�@���� exp �̕ϐ��� logx / x �Ƃ��Ă݂܂��F
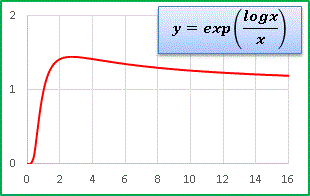
�@���Ȃ�����̂�����ł��B�O���t�ł͏��������ɂ����ł��� [0, 0.3] ������ł� x ���ɂׂ�����ƒ���t���Ă��܂��B���̂��Ɣ�r�I�傫�Ȍ��z�Œl���������Ă����܂����Ax ���傫���Ȃ�Ƃ����Ɍ��z���ɂ߂Ȃ���ɂ₩�Ȍ����ɓ]���܂��B
�@
�O���t�̊T�`���Ώ̂ɕς��܂�
�@e �̌��� x �� 2 �������悹�܂��Fy = exp(�|ax2 + bx)�@�ia > 0, b �͔C�Ӂj
�@�܂��� b = 0 �Ƃ��� a ��ω������Ă݂܂��F
�@
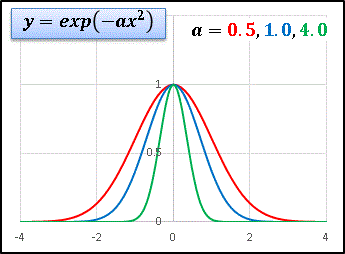
�@�}�ł� a = 0.5, 1.0, 4.0 �ɑΉ�����O���t��F�������ĕ\�����Ă��܂��B
�@�ő�l�� 1 �ɌŒ肳��Ă��܂����A a �̒l���������ɎR���������Ȃ��Ă��܂��ˁB
�@���� a = 1 �Ƃ��āAb ��ω������Ă݂܂��傤�F
�@
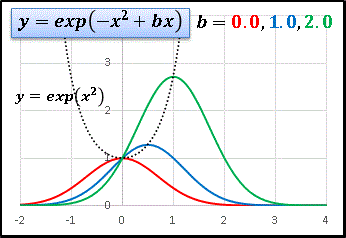
�@b = 0.0, 1.0, 2.0 �ƕω������Ă��܂��B
�@���x�� b �̑����ɍ��킹�ăO���t���E�ֈړ�����Ɠ����ɍő�l���傫���Ȃ��Ă����܂��B�v�Z���K�����˂āA���̍ő�l�̈ʒu�����߂Ă݂܂��傤�B
y��= (�|2 x + b) exp(�|x2 + bx)
�ł�����Ay��= 0 �Ƃ����A�ő�l���Ƃ� x ����эő�l��
x = b/2,�@�ő�l ymax = exp(b2/4)
�ƂȂ�܂��B�ő�l�� b2 �̎w�����Ƃ��đ������Ă��܂��B�}�ɂ͍ő�l�̈ړ��������_�����`����Ă��܂��ˁB���̋Ȑ��� b = 2x �̊W��p����
y = exp(x2)
�Ƌ��߂邱�Ƃ��ł��܂��B
�@���� exp(�|x2) �� xn ���悶�Ă݂܂��F
�@
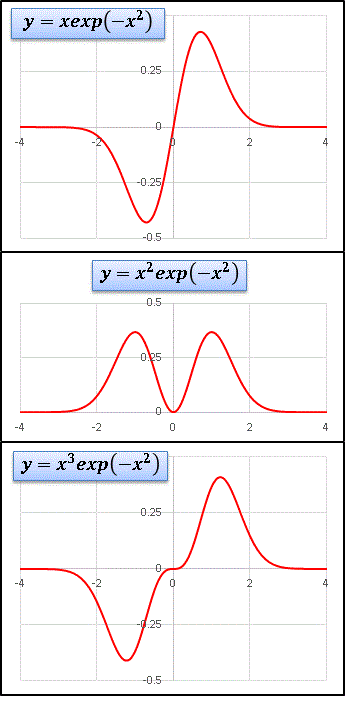
�@exp(�|x2) ������ł�����Ax, x2, x3 ���|����ƁA����A����A����ƕω����܂��B�ł͖��������|������ǂ��Ȃ�ł��傤���H�͈͂� x > 0 �ɐ������ăO���t��`���Ă݂܂��傤�F
�@
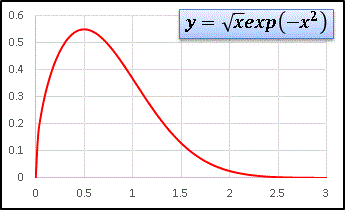
�@�����オ��̑������ŁAx = 0.5 �ɂ�����ő�l�܂ň�C�ɋ삯�オ���āA���̂��Ƃ͔�r�I�Ȃ��炩�ɒl�𗎂Ƃ��Ă����܂��B���������悶��ƁA���̂悤�ɃO���t�̊T�`���Ώ̂ɕς��܂��B�ő�l���Ƃ� x �͐���Ɠ����悤�ɊȒP�Ȍv�Z�œ����܂��̂Ŏ����Ă݂Ă��������B
�@ �@