久しぶりの演習問題です。今回は 18 世紀のイタリアの女性数学者、 アニェージ(アーネシ) さんが発見した曲線を題材にしました。
問題54 アニェージの曲線(アーネシの曲線) [高3★★★☆☆]
図のように原点に接するように直径 a の円を置きます。原点から円を 2 等分するように垂線を引いて円と交わる点 C をとり、線分 OC に沿うように y 軸を設定します。また C に接するように x 軸に平行な直線 L1 を引きます。そして原点 O から円周上の点 A に線分 OA を引き、その延長戦が L1 と交わる点を B とします。さらに B から線分 OC に平行な直線 L2 を引き、点 A から x 軸に平行にのばした線が L2 を交わる点を P とします。

(1) A が円周上を動くとき、P の座標を θ で表してください。
(2) (1) で求めた式から θ を消去して P の描く曲線を y = f(x) の形で表してください。
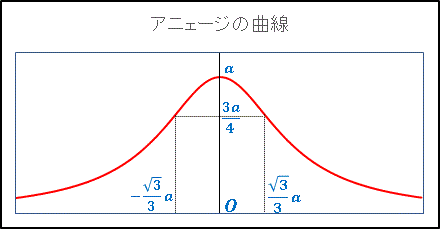
(3) 曲線 y = f(x) の概形を描いてください。(変曲点の位置も明示してください)
≫ [Amazon書籍] もういちど読む数研の高校地学
解答54(cosθ と tanθ の間に成り立つ公式を思い出します)
(1) 下図のように線を引きます。
x = BC ですから、x = atanθ はすぐにわかります。
y は図の AN に相当します。 OA の長さを求めると、
OA = 2・(a/2)cosθ = acosθ
なので、
AN = OA cosθ = acos2θ
となります。よって P の座標は
(x, y) = (atanθ, acos2θ)
となります。
(2) cosθ と tanθ の間に成り立つ公式を思い出します。
に tanθ = x/a, cos2θ = y/a を代入して
を得ます。
(3) 商の微分公式によって y と y' を計算すると、
となるので、 y = 0, y' = 0 より
極 値
変曲点
となります。増減表とグラフは下図のようになります。

18 世紀のリケジョさんです
今でこそリケジョ(理系女子)さんは普通に(?)見かけますが、時代が 18 世紀まで遡ると、それはもう大変に珍しい存在でした。マリア・ガエターナ・アニェージ (Maria Gaetana Agnesi) はそうした稀有な数学者で、女性としては史上2人目の大学教授です。男女平等などという概念など欠片も存在しなかった時代ですから、生半可な才能では大学教授までには登り詰められなかったはずです。
アニェージは紛れもなく神童であり、幼少の頃から優れた語学の才能を見せ、11 歳でギリシャ語やラテン語、ヘブライ語など七ヶ国語を話すことができたそうです。数学と関係ないと思われるかもしれませんが、他の天才たちにもみられるように、語学の才能と数学の才能は密接に関係しているようなのです。
アニェージは家庭環境にも恵まれていました。父親のピエトロは大富豪でしたが、身分が低いことを気にしていて「子供たちに英才教育をほどこして一族を名門にしてやるぞ」というものすごい野心をもっていましたから、アニェージはその才能を存分に伸ばして数学者として大成することができたのです。
彼女は専門である「微分・積分」の教科書を執筆しました。
しかもなんとこれが世界初の「微積」の教科書と言われています。
当時は現在とは違って、数学の教科書というものはあまり普及していなかったので(そもそも書物自体が貴重でした)、すぐに評判が広まり、フランス語訳と英語訳でも出版されました。