途方もなく長い周期をもつ振動関数
y = cos[log(1 + x)] はとても 長い周期 をもつ振動関数です。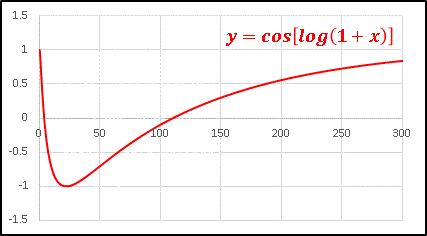
半端な長さじゃありませんよ。 x の大きいところでは対数関数の増加率が小さいので、その周期は途方もなく長いのです。試しに x = 35000 まで範囲を拡大してみても ......
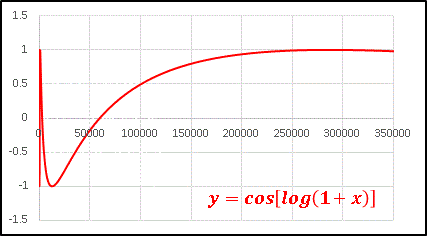
これでもまだ数回しか振動していないことがわかります。
次は log の中身に sinx を組込んで y = cos[log(1 + x + sinx)] としてみましょう。
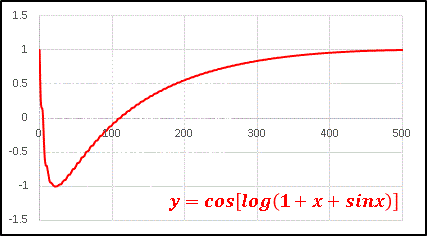
sinx の寄与が小さいので、ノイズのように小刻みに振動させますが、x が大きくなってくると、その揺れも小さくなります。
最後は y = cos[log(1 + x2 + x sinx)] という関数です。
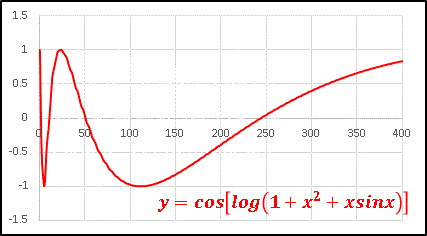
x2 の効果で最初のうちは何度か振動しますが、それもやがて log で抑え込まれて長周期関数となります。